Тензор кривизны Римана - Кристоффеля

Согласно определению тензора необходимым и достаточным его признаком является тензорный закон преобразования компонент при переходе от одной КСК к другой. Однако проверять этот закон каждый раз - это трудоемкая и не простая задача, особенно для многовалентных тензоров. Оказывается, что можно ввести другой тензорный признак по следующей теореме.

ТЕОРЕМА О ЧАСТНОМ. (Необходимый и достаточный признак тензора.)

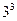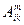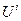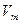Пусть в некоторой системе координат задано, например, функций вида . Если при произвольном выборе двух векторов (тензоров первой валентности и тензорное умножение и последующая свертка вида

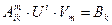(11.1)

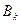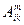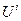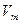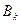дает вектор (тензор) , то множество образует тензор третей валентности дважды ковариантный и раз контравариантный. Докажем достаточное условие. Так как , и тензора, то для них справедливы тензорные законы:

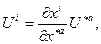
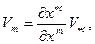
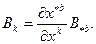
Равенство (11.1) имеет место в старой и новой КСК, тогда:

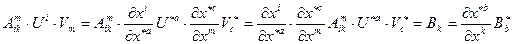
Из этих преобразований следует, что

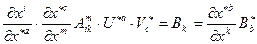
Домножим это равенство на 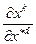, свернем по индексу 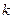и воспользуемся свойством тензора Кронеккера (9.11).

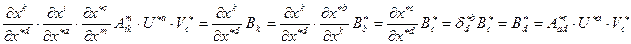
Таким образом, необходимо сравнить левую и правую части последнего равенства.

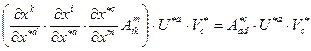
Отсюда, в силу произвольности исходных векторов 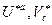, получаем

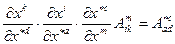(11.2)

тензорный закон преобразования для смешенного тензора третьей валентности дважды ковариантного и раз контравариантного, что и требовалось доказать.

Поставим вопрос о производной второго порядка от контравариантного тензора первой валентности, для этого вычислим:

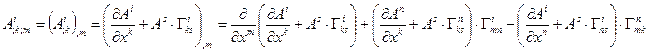
Раскроем скобки и перегруппируем слагаемые:

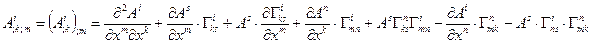
Поменяем порядок дифференцирования компоненты 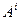- вначале по 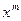, а потом по 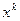и вычтем полученное выражение из предыдущего. Формально это означает, что необходимо поменять местами индексы 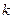и 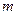, согласовать индексы суммирования (переставить 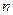и 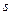, где это требуется) и учесть то, что вторая смешанная производная не зависит от порядка дифференцирования.

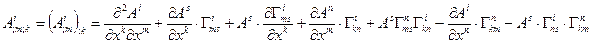
В результате получим:

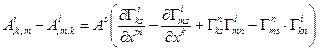(11.3)

В равенстве (11.3) слева стоит тензор третей валентности (он получен как разность двух тензоров), справа компоненты произвольного тензора 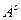умножаются на скобку, в которой по теореме о частном также стоит тензор четвертой валентности трижды ковариантный и раз контравариантный. Этот тензор играет важную роль в теории пространств и называется тензором кривизны Римана-Кристоффеля.

ОПРЕДЕЛЕНИЕ 11.1.Тензором Римана-Кристоффеля называется тензор четвертой валентности посторинный с помощью символов Кристоффеля, например, по следующему правилу:

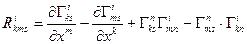(11.4)

Теперь мы уже знаем, что символы Кристоффеля не являются тензорами и может показаться странным, что из нетензорных объектов строится тензор. Однако следует вспомнить, что при определении тензора кривизны используется частная производная которая сама по себе не тензорная операция. Особенность 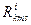в том, что в ДСК все его компоненты тождественно обращаются в нуль, т.к. 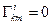. Это означает (см. тензорный закон), что в любой другой КСК тензор кривизны также тождественно равен нулю. В таком случае возникает вопрос, зачем нужен нулевой тензор и какой в этом смысл? Ответ на этот вопрос состоит в том, что построить ДСК возможно только в плоских Евклидовых пространствах, кривизна которых равна нулю. Если пространство имеет кривизну отличную от нуля, то мы не можем построить ДСК и вынужденны пользоваться только КСК. Можно строго доказать [7], что двукратная свертка 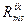дает инвариант пропорциональный гауссовой кривизне пространства.

ОПРЕДЕЛЕНИЕ 11.2 Римановыми (искривленными) пространствами называют метрические пространства с отличным от нуля тензором кривизны.

В теории метрических пространств существует понятие вложения одного пространства в другое. Оказывается, что любое риманово пространство 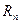можно вложить в евклидово 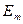большей размерности, например, двумерная сфера в трехмерный плоский куб. В общем случае такое вложение возможно, если выполняется ряд условий и размерность плоского 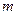и искривленного 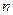пространств связаны между собой следующим соотношением: 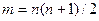. Отсюда видно, что трехмерное пространство Римана 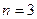можно вложить в шестимерное пространство Евклида 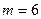. Основываясь на теории вложения пространств, удается найти взаимно однозначное соответствие между точками плоского и искривленного пространств. Таким образом, с математической точки зрения все процессы можно описывать как в искривленных, так и плоских пространствах разной размерности. Следует однако, сказать откровенно о том, что мы с вами вторглись в трудно проходимую область теории пространств и еще не обладаем достаточным запасом знаний, чтобы легко и непринужденно по ней двигаться. Поэтому благоразумней, с нашей точки зрения, этим здесь ограничиться и обсудить вопрос о кратчайших расстояниях в пространствах Римана. Для любопытных можем предложить почитать об этом в рекомендуемой литературе [8] и [9].