Главные направления и кривизны поверхности
Исследуем теперь вопрос, как меняется нормальная кривизна в зависимости от направления её вектора скорости. Как и для всякой квадратичной формы, для второй квадратичной формы найдётся ортонормированный базис в касательной плоскости, в котором форма имеет диагональный вид 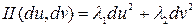 .
.
Определение 3.5. Направления, задаваемые векторами этого базиса, называются главными направлениями, а числа 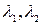 – главными кривизнами.
– главными кривизнами.
Определение 3.6. Произведение 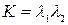 называется гауссовой или полной кривизной поверхности в данной точке, полусумма
называется гауссовой или полной кривизной поверхности в данной точке, полусумма 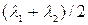 – средней кривизной.
– средней кривизной.
Знание главных кривизн и главных направлений позволяет найти нормальную кривизну в произвольном направлении по формуле
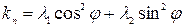 ,
,
где 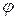 – угол между данным направлением и направлением первого базисного вектора (формула Эйлера).
– угол между данным направлением и направлением первого базисного вектора (формула Эйлера).
Из формулы Эйлера следует экстремальное свойство главных направлении: это те направления, где нормальная кривизна принимает наибольшее или наименьшее значение. Это свойство помогает находить главные направления: вектор с координатами du, dv задаёт главное направление, если выполнено условие:
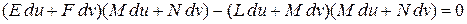 .
.
Главные кривизны ищутся из условия 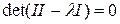 , т.е. из уравнения
, т.е. из уравнения 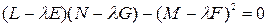 .
.
Дата добавления: 2016-06-02; просмотров: 3072;
