Площадь поверхности

Через первую квадратичную форму можно определить площади любых участков поверхности. Пусть f – гладкая поверхность, заданная уравнениями

x=x(u, v), y=y(u, v), z=z(u, v)

и D – область на ней, ограниченная конечным числом кусочно-гладких кривых.

Тогда площадь поверхности вычисляется по формуле:

.

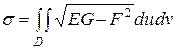Заметим, что если 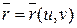– векторная функция, т.е. 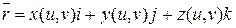, то в любой точке M(u, v) поверхности имеем:

.

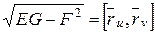Следовательно, площадь поверхности можно вычислить по формуле:

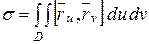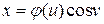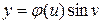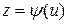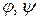Задача 3.1. Найти первую квадратичную форму поверхностного вращения , , , где – функции, имеющие непрерывные производные.

Решение. Имеем , , 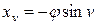, 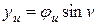. Тогда

,

,

.

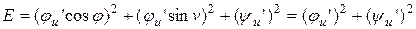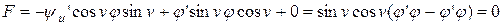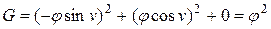Таким образом, первая квадратичная форма имеет вид

. ■

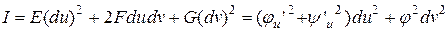Мы видим, что зная первую квадратичную форму, можно решать метрические задачи, т.е. задачи на вычисления.

В связи с этим говорят, что первая квадратичная форма задаёт метрику поверхности и её часто называют линейным элементом поверхности. Первая квадратичная форма описывает поверхность в первом приближении, когда малый участок поверхности заменяется на участок касательной плоскости.

Все факты, которые могут быть получены путём измерении на поверхности с помощью первой квадратичной формы, относятся к так называемой внутренней геометрии поверхности.