Измерение на поверхности длин, углов, площадей. Первая квадратичная форма поверхности
Для решения многих физических, технических и геометрических задач нужно уметь вычислять длины дуг, лежащих на поверхности, углы между такими дугами, площади тех или иных частей поверхности.
Основная идея всех излагаемых в этом параграфе рассуждений состоит в замене бесконечно малого элемента гладкой поверхности соответствующим элементом касательной плоскости. Поэтому полезно начать с некоторых формул и понятий, относящихся к вычислению длин, углов и площадей на плоскости.
Перейдем к изучению поверхности в бесконечно малом, вблизи какой-нибудь её точки M(x, y).
Вычислим дифференциал вектора 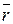 вдоль кривой. Тогда
вдоль кривой. Тогда 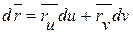 , где
, где 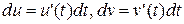 . Найдём скалярные квадраты левой и правой частей этого равенства:
. Найдём скалярные квадраты левой и правой частей этого равенства: 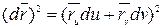 или
или
|
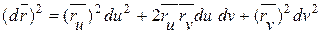 .
.
Введём для этих скалярных произведений сокращённые обозначения:
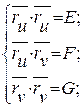 или в координатах
или в координатах
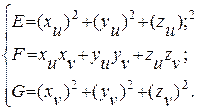
|

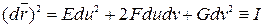 .
.
Выражение (3.8), называется первой квадратичной формой на поверхности и играет важную роль в теории поверхностей.
Первая квадратичная форма служит прежде всего для измерения бесконечно малых дуг на поверхности. Далее посредством интегрирования, нетрудно перейти к точному вычислению длин на поверхности.
Пусть задана часть кривой на поверхности: u=u(t), v=v(t), где 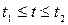 .
.
Тогда длина части кривой на поверхности выражается формулой:

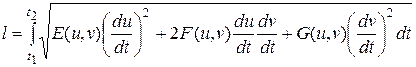 .
.
Зная первую квадратичную форму на поверхности, можно находить и углы между кривыми.
Определение 3.4. Углом между кривыми 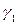 и
и 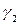 называется угол между касательными к этим линиям в их общей точке M.
называется угол между касательными к этим линиям в их общей точке M.
Пусть 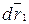 и
и 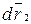 – векторы касательных к линиям
– векторы касательных к линиям 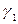 и
и 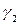 в точке M. Тогда
в точке M. Тогда  или, в координатах, учитывая, что
или, в координатах, учитывая, что 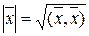 для произвольного вектора
для произвольного вектора 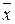 , имеем
, имеем
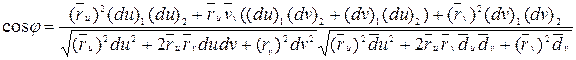 или
или
|
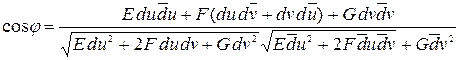 .
.
Дата добавления: 2016-06-02; просмотров: 2155;
