Вторая квадратичная форма поверхности
Вторая квадратичная форма описывает поверхность во втором приближении. Она показывает, как отклоняется поверхность от касательной плоскости и полностью определяет кривизну поверхности. Можно было бы само понятие второй квадратичной формы ввести, исходя из задачи о вычислении расстояния от точки поверхности до касательной плоскости, проведенной через близкую точку.
Пусть f – регулярная поверхность, заданная уравнением 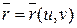 , а
, а
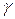 – линия на этой поверхности. Имеем
– линия на этой поверхности. Имеем 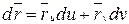 . Введём вектор нормали
. Введём вектор нормали 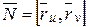 , тогда единичный вектор нормали в точке M к поверхности f имеет вид
, тогда единичный вектор нормали в точке M к поверхности f имеет вид 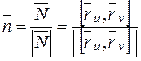 . Найдём квадратичную форму
. Найдём квадратичную форму 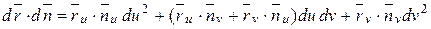 . Так как
. Так как 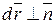 , то скалярное произведение
, то скалярное произведение 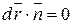 и, следовательно,
и, следовательно, 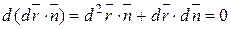 .
.
Отсюда
|
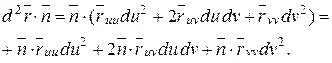
Здесь учтено, что 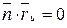 ,
, 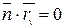 , т.е. отсутствуют слагаемые с этими произведениями.
, т.е. отсутствуют слагаемые с этими произведениями.
Введём обозначения 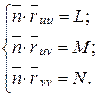
или в координатах: 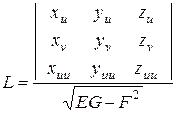 и аналогично,
и аналогично,
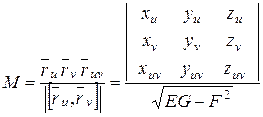 ,
, 
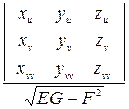 .
.
Замечание 3.3. Здесь 
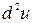 – дифференциал второго порядка и
– дифференциал второго порядка и 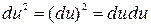 – квадрат дифференциала.
– квадрат дифференциала.
|
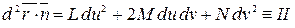 .
.
В формуле (3.12) правая часть равенства называется второй квадратичной формой поверхности.
Замечание 3.4. В частности, если поверхность задана явным уравнением 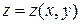 , то
, то 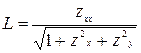 ,
, 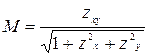 ,
, 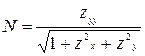 .
.
Дата добавления: 2016-06-02; просмотров: 1778;
