Лекция 10 Дифференцирование базисных векторов

Вернемся к вопросу о построении произвольной КСК. Ковариантные базисные вектора, по определению, являются функциями точки, т.е.

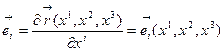(10.1)

поэтому правомерен вопрос об изменении этих векторов вдоль соответствующих координатных линий КСК. Это означает, что мы должны рассмотреть частную производную от базисного вектора, например, в собственном базисе. Коэффициенты разложения необходимо нумеровать тремя индексами: номер компоненты, номер координаты по которой ведется дифференцирование и номер вектора

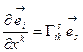(10.2)

Набор функций 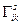(27 штук) играет важную роль в теории пространств и называется символами Кристоффеля второго рода. Если задуматься, то станет очевидным, что символы Кристоффеля не могут быть тензорами в общем случае, т.к. они тождественно обращаются в нуль в ДСК, где базисные вектора фиксированы. Чтобы убедится в этом, построим закон преобразования 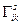при переходе от одной КСК к другой. Пусть по-прежнему 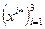-- новая КСК, 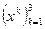-- старая КСК, в которых справедливо разложение (10.2):

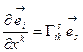- в старой КСК и 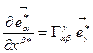- в новой КСК (10.3)

Так как 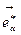базисный вектор, то для него справедлив закон: 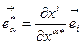. Продифференцируем это равенство по координате 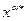: 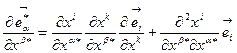и подставим (10.3), получим: 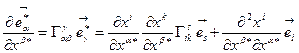. Во втором слагаемом индекс суммирования 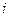меняем на 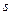, а вектор 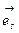преобразуем по обратному тензорному закону, тогда

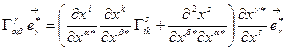
Используя линейную независимость базисных векторов, приравняем коэффициенты при :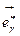

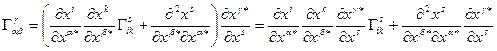(10.4)

Это и есть закон, по которому преобразуются символы Кристоффеля второго рода при переходе от одной КСК к другой. Очевидно, что этот закон не совпадает с тензорным. Таким образом, в общем случае символы Кристоффеля второго рода не образуют тензор. Следует, однако, заметить, что в так называемых аффинных пространствах, где допускаются только линейные координатные преобразования, множество 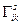становится тензором, так как вторые смешанные производные в (10.4) тождественно обращаются в ноль. Поэтому принято называть символы Кристоффеля афинным тензором третьей валентности.

Свойство. Символы Кристоффеля второго рода симметричны по нижним индексам. Чтобы доказать это, продифференцируем определение (10.1) по координате .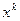

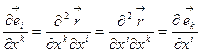
Учитывая разложение (10.2), делаем вывод о том, что 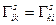(10.5)