Волновые процессы в однородной длинной линии
Представим коэффициент распространения линии в алгебраической
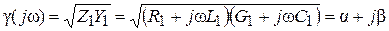 , (6.12)
, (6.12)
а волновое сопротивление линии и постоянные интегрирования в показательной формах:
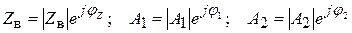 . (6.13)
. (6.13)
Подставим выражения (6.12 и 6.13) в (6.6 и 6.8)
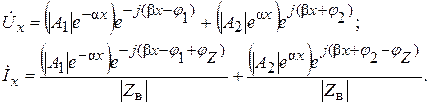
Переходя от комплексных значений напряжения и тока к мгновенным, получим
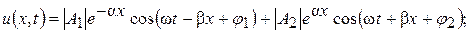 (6.14)
(6.14)
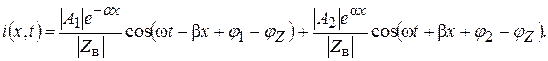 (6.15)
(6.15)
Вид выражений (6.14 и 6.15) для напряжения и тока одинаков, поэтому анализ сначала будет проведен для напряжения.
Установившееся значение напряжения (6.14) можно представить в виде алгебраической суммы двух подобных по структуре, но отличающихся знаками перед коэффициентами α и β гармонических составляющих:
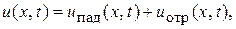
где
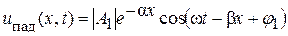 – падающая волна напряжения;
– падающая волна напряжения;
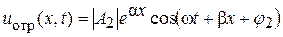 – отраженная волна напряжения.
– отраженная волна напряжения.
При фиксированном x каждая из составляющих напряжения (тока) представляет собой гармоническую функцию времени t. Для каждого фиксированного момента времени t напряжение uпад(x, t) изменяется вдоль линии по гармоническому закону, причем оно уменьшается по амплитуде с ростом x (в сторону от генератора к нагрузке) по экспоненциальному закону (см. рис. 6.3, а).
При увеличении t точки этого напряжения, имеющие одинаковую фазу, смещаются в сторону нагрузки. Поэтому составляющую напряжения (тока), распространяющуюся от генератора в направлении нагрузки, называютпадающей волной напряжения (тока).
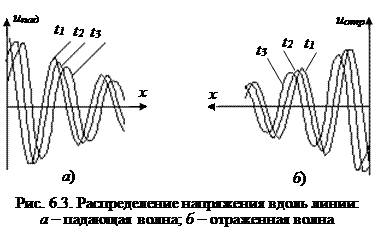 |
Второе слагаемое uотр(x, t) в напряжении (6.14) представляет собой волну напряжения, распространяющуюся от нагрузки в направлении генератора (рис. 6.3, б). Эту волну называютотраженной волной напряжения. Амплитуда отраженной волны также уменьшается в сторону распространения волны (от нагрузки к генератору).
Таким образом, мгновенное значение напряжения в любой точке линии определяется суммой падающей и отраженной волн напряжения.
Сказанное относительно мгновенного значения напряжения относится и к мгновенному значению тока
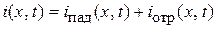 .
.
Совокупность падающей волны напряжения и падающей волны тока называют падающей волной, а совокупность отраженных волн напряжения и тока – отраженной волной.
Амплитуды падающей и отраженной волн уменьшаются в направлении распространения волн по закону e-αxи eαx соответственно. Величина α, характеризующая уменьшение амплитуды на единицу длины линии, называется коэффициентом ослабления и определяется
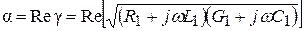 . (6.16)
. (6.16)
Убывание амплитуды волны связано с потерями энергии в резистивных элементах модели отрезка линии R1 и G1. В идеальной линии, т.е. линии без потерь (R1 = G1 = 0) коэффициент ослабления α = 0, а коэффициент распространения является чисто мнимым: 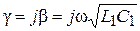 .
.
Амплитуды падающей и отраженной волн напряжения и тока в линиях без потерь не зависят от координаты x и не изменяются вдоль линии.
Мнимая часть комплексного коэффициента распространения (6.12)
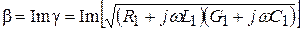 ,
,
характеризующая изменение фазы прямой и обратной волн на единицу длины линии, называется коэффициентом фазы.
В связи с тем, что напряжение и ток в любом сечении линии можно рассматривать как результат наложения двух волн – падающей и отраженной, нетрудно придти к заключению, что слагаемые, входящие в выражения (6.6), (6.8), представляют собой комплексные значения напряжения или тока падающей и отраженной волн
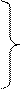
 (6.17)
(6.17)
 где
где 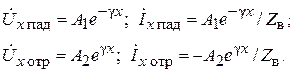 (6.18)
(6.18)
Дата добавления: 2016-11-02; просмотров: 1491;
