Преобразования базисов.

В первой части нашего курса мы изучали, в основном, скалярные и векторные поля и только в последних лекциях появилось понятие тензора (ФМТГ). Во второй части курса будут рассмотрены поля более сложной природы - тензорные, как единый класс объединяющий большинство известных в физике полевых понятий. Вспомним описание скаляра и вектора. Для задания скалярной величины достаточно одного числа, т.е. скаляр математически отображается точкой на числовой оси. Вектор, как более сложный объект, удается отобразить с помощью направленного отрезка (геометрическое описание) или набора трех его проекций (координатное представление). В дальнейшем оказалось, что координатное описание вектора является более универсальным, так как направленный отрезок можно построить не всегда (например, на сферической поверхности). При этом возникает сложность, связанная с тем, что в различных системах координат проекции одного и того же вектора имеют различный вид. Этот вопрос становится еще более запутанным при переходе к произвольным КСК, так как базисы их становятся функциями точки. Другими словами, произвольная КСК становится локальной и возникает проблема сравнения компонент вектора в двух бесконечно близких точках. Разрешение этой проблемы связано с определением параллельного переноса вектора. Об этом мы подробнее поговорим позже, а сейчас, чтобы избежать излишних сложностей, положим в основу определения, например, вектора его признак не зависящий от выбора КСК. Оказалось, что в качестве такого признака разумнее всего выбрать закон преобразования компонент вектора при переходе от одной КСК к другой. Получить этот закон проще всего для базисных векторов.

ОПРЕДЕЛЕНИЕ 8.1. Ковариантным (контравариантным) тензорным законом преобразования компонент тензора (тензорный закон) называется правило, по которому преобразуются ковариантные (контравариантные) базисные вектора при переходе от одной произвольной КСК в другую.

1. Определим тензорный закон для 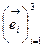. Пусть заданы две КСК: 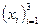- старая (условно) и 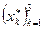- новая, между которыми существует взаимно однозначное соответствие: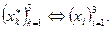

Обратите внимание: старые и новые координаты различаются не индексами, а наличием или отсутствием "*". По определению ковариантного базиса имеем:

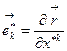-новый, 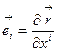- старый. (8.1)

Учитывая зависимость радиус-вектора от криволинейных координат, следует рассматривать как сложную вектор-функцию старых координат, тогда, по определению сложной производной от радиус-вектора по старой координате, имеем: 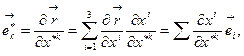или,

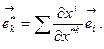(8.2)

Мы получили прямой тензорный закон преобразования ковариантных базисных векторов. Обратный тензорный закон для этих же векторов имеет следующий вид:

или, 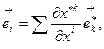(8.3)

2. Определим тензорный закон преобразования для контравариантного базиса. Пусть

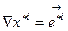-новый базис, 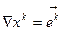старый базис, 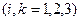Разложим вектор 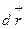в старом и новом базисах. Тогда, по определению компоненты в каждой КСК имеем:

и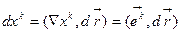

Вычислим 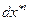, используя зависимость между старыми и новыми координатами:

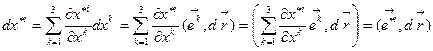
Отсюда следует, что 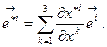(8.4)

Мы получили прямой тензорный закон преобразования контравариантных базисных векторов. Предлагаем читателю самостоятельно вывести обратный тензорный закон для этого базиса:

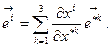(8.5)

Сравним тензорные законы (8.2) и (8.4). Легко доказать, что они взаимно обратны в том смысле, что коэффициенты преобразования базисных векторов образуют взаимно обратные матрицы. В самом деле, при матричном умножении имеем: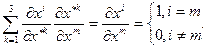

Эта закономерность в тензорных законах объясняет принятую терминологию: ковариантные – значит прямо преобразующиеся, контравариантные - обратно преобразующиеся вектора.

Определим тензорный закон преобразования компонент произвольного вектора 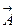в ковариантном базисе. Для этого разложим его по формуле (5.10), в которой мы заранее пронумеровали 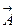проекции верхними индексами, считая, что они преобразуются по контравариантному закону. Проверим наше предположение, расположив индексы у компонент сначала посредине и сместив их после установления закона преобразования:

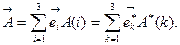
Заменим 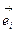по формуле (8.3):

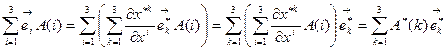
Из линейной независимости базисных векторов следует, что

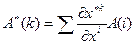. (8.6)

Очевидно, что правило (8.6) соответствует тензорному закону преобразования контравариантных векторов, поэтому индексы в формуле (8.6) следует сместить вверх. Используя этот метод, просто вывести правило преобразования компонент вектора, полученных в контравариантном базисе; не трудно сообразить, что они будут преобразовываться по ковариантному закону. Таким образом,

тензорные законы преобразования базиса и компонент вектора в этом базисе взаимно противоположны, чем и объясняется принятая терминология (см. определения 6.1. и 6.2). Это следует хорошо запомнить и при разложении вектора в КСК индексы у проекций и базисных векторов писать противоположно.

Определим тензорный закон преобразования компонент ФМТГ. По определению 6.3.

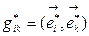- новая КСК, 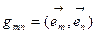старая КСК. Преобразуем старый базис по формуле (8.2) и подставим в 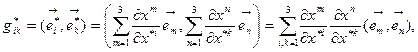или окончательно

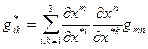(8.7)

Это и есть искомый тензорный закон преобразования ФМТГ в ковариантной форме. Аналогичным образом легко получить закон преобразования ФМТГ в контравариантной форме. Пусть

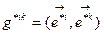- новая КСК, 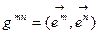старая КСК, тогда

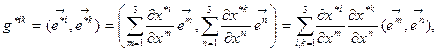или, окончательно,

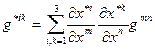(8.8)

А это - тензорный закон преобразования ФМТГ в контравариантной форме. Рассмотрим ФМТГ в смешанной форме:

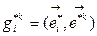- новая КСК, 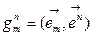- старая КСК, тогда

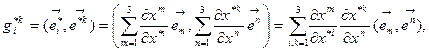или окончательно

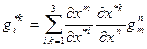(8.9)

Что представляет тензорный закон преобразования ФМТГ в смешанной форме.

Анализ тензорных законов для векторов и тензоров позволяет сделать некоторые общие выводы. Во-первых, необходимо обратить внимание на то, что во всех выражениях, где стоит знак суммы, индекс суммирования встречается дважды. Это обстоятельство дает возможность сформулировать правило Эйнштейна.

ПРАВИЛО ЭЙНШТЕЙНА. Для упрощения записи выражений, где встречается знак суммирования по повторяющимся индексам, подразумевается суммирование без указания символа суммы 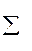. Во-вторых, самым важным свойством тензорного закона является то, что его вид

одинаков для любой пары КСК. Это свойство было положено в основу общего определения тензорных величин и называется инвариантностью.

ОБЩЕЕ ОПРЕДЕЛЕНИЕ ТЕНЗОРА. Пусть задано 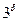функций вида 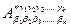в новой КСК, 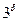- функций вида 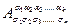- в старой КСК. Если эти функции при переходе от одной КСК к другой преобразуются по следующему тензорному закону

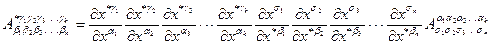(8.10)

то они образуют 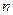- раз ковариантный и 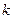- раз контравариантный тензор валентности 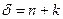Еще раз следует напомнить, что по повторяющимся индексам 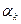и 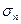подразумевается

суммирование. Иначе говоря, тензор любой валентности всегда можно представить множеством некоторых функций (необходимое условие), которые преобразуются по тензорному закону (8.10.) при переходе от одной КСК к другой (достаточное условие). Это определение оказалось очень плодотворным и позволило объединить большое число физических понятий в единый класс - тензоры. Так, например, если мы имеем набор, состоящий из одной функции, которая сохраняет свое значение в одной и той же точке пространства в любой КСК, то это тензор нулевой валентности или скаляр (инвариант); вектор - набор, состоящий из трех функций, преобразующихся по ковариантному (8.3) или по контравариантному (8.5) законам, он же тензор первой валентности; ФМТГ представляет собой множество из девяти функций с тензорным законом преобразования (8.8)-(8.9) и называется тензором второй валентности и т.д. Таким образом, тензор - это единый объект, описывающий те или иные физические или математические

свойства системы. Он может быть представлен в различных формах, в зависимости от валентности, набором функций, преобразующихся при переходе от одной КСК к другой по тензорному закону (8.10).

Упражнение 8

1. Используя координатные преобразования Лоренца

,

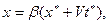
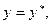
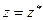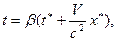
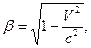
найти тензорные законы преобразования для тензоров первой и второй валентности.

2. Определить при каких условиях частная производная от компоненты тензора первой валентности по координате будет тензором второй валентности.

3. Составить матрицы координатных преобразований базисных векторов: при переходе от декартовых координат к сферическим и обратно; при переходе от декартовых к цилиндрическим и обратно.

4. Записать матрицу преобразования компонент вектора: при отражении трех координатных осей при повороте декартовой системы координат вокруг оси на угол .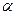

5. Построить тензор инерции в декартовой системе координат для абсолютно твердого тела, вращающегося вокруг неподвижной оси с произвольной угловой скоростью.