Выражение дивергенции в ортогональной КСК

Воспользуемся тем, что вывод дивергенции не должен зависеть от выбора первоначальной поверхности и способа стягивания ее в точку. В качестве первоначальной замкнутой кусочно-гладкой поверхности возьмем малый (в пределе бесконечно малый) параллелепипед 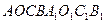. Предельным переходом будем стягивать его в точку O. Для упрощения записи громоздких выражений введем обозначения граней (см. рис. 8).

Рис. 8 Вычисление дивергенции в КСК

.

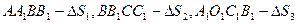
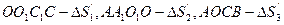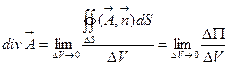. (7.9)

Здесь 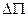- поток вектора 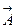через полную поверхность параллелепипеда. Очевидно, что его можно разбить на сумму 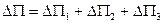- суммарный поток вектора через противоположные грани 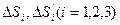. Вычислим, например,

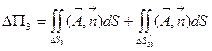(7.10)

Каждая грань параллелепипеда при 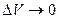становится бесконечно малой, поэтому с точностью до второго порядка малости на каждой грани будет справедливо следующее утверждение: на

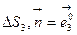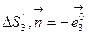на . Интегралы в (7.10) вычислим, используя определение проекции вектора и теорему Лагранжа о среднем: 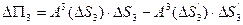(7.11)

Здесь 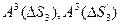- проекции вектора 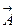на орт 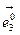, заданные на соответствующих гранях.

Для бесконечно малых параллелограммов 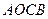и 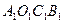с принятой точностью можно записать:

.

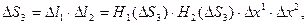
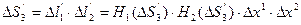Подставим этот результат в (7.11) и после несложных преобразований получим

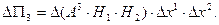(7.12)

Здесь обозначено 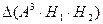- приращение функции, стоящей в скобках, при переходе с грани 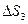на грань 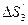Подобным образом подсчитаем поток вектора через остальные противоположные грани.

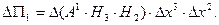(7.13)

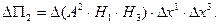(7.14)

Полный поток вектора 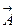получим, просуммировав выражения (7.12)-(7.14):

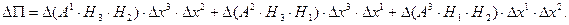
Легко подсчитать объем параллелепипеда с точностью до второго порядка малости

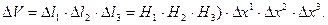
Дивергенцию вектора вычислим, подставляя и в определение (7.9):

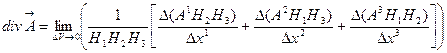. (7.15)

Стремление объема к нулю, с одной стороны, дает значение всех функций, стоящих под знаком предела, в предельной точке O, с другой стороны, предел отношения приращения функции к приращению аргумента по определению есть частная производная. Таким образом, окончательно дивергенция будет иметь следующий вид в ортогональной КСК:

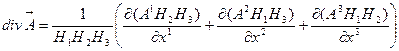. (7.16)