Матрица перехода от старого базиса к новому

Пусть в пространстве R имеются два базиса: старый 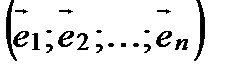и новый 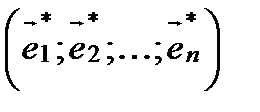. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

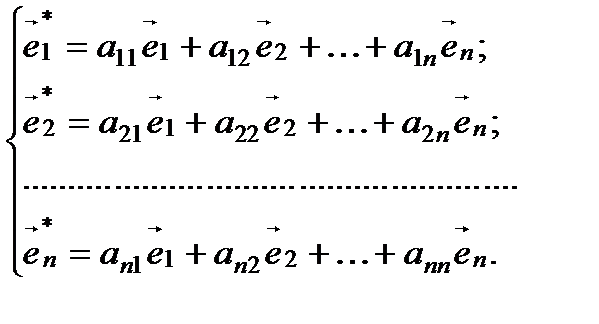(2)

Полученная система означает, что переход от старого базиса 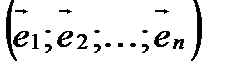к новому 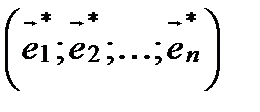задаётся матрицей перехода:

,

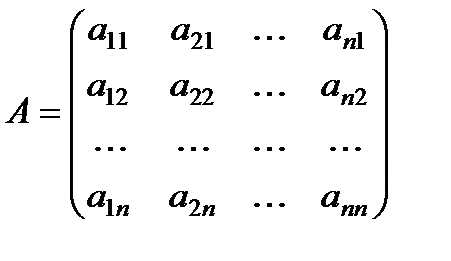причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

Обратный переход от нового базиса 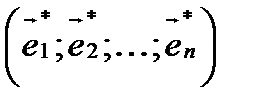к старому базису 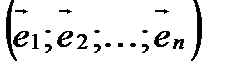осуществляется с помощью обратной матрицы .

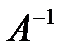Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 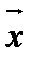имеет координаты 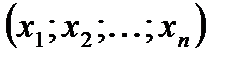относительно старого базиса и координаты 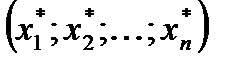относительно нового базиса, т.е.

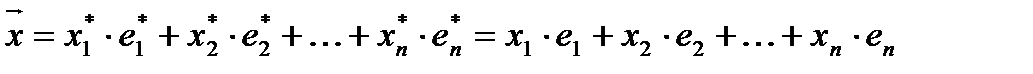(3)

Подставив значения 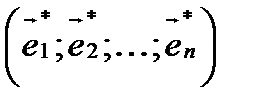из системы (2) в левую часть равенства (3), получим после преобразований:

,

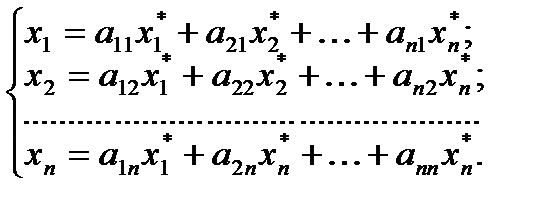т.е. в матричной форме

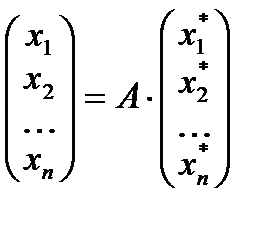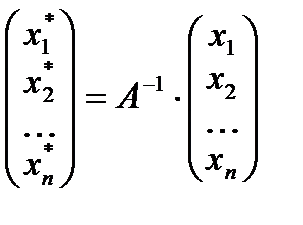или (4)

Пример 51.В базисе 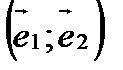даны векторы 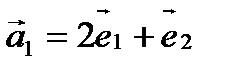, 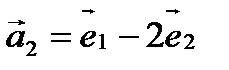. Доказать, что векторы 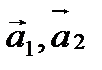- образуют базис;

найти координаты вектора 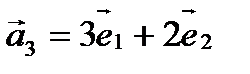в базисе .

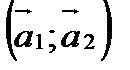Решение: 1) векторы образуют базис, если они линейно независимы. Составим векторное равенство: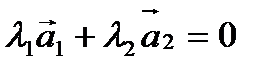

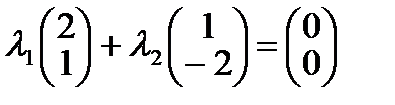
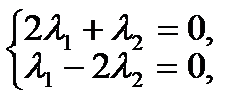Решим данную систему методом Гаусса: ~

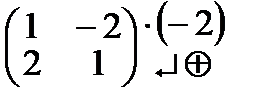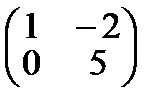
Получим: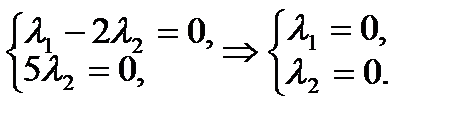

Убедились в единственном нулевом решении системы, а значит - образуют базис.

2) Выразим связь между базисами и :

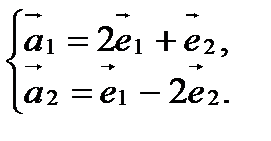
В соответствии с формулами (4) перехода от старого базиса к новому: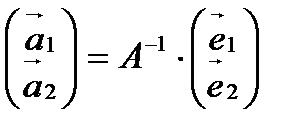

Матрица перехода имеет вид: .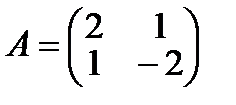

(Обращаем внимание на то, что коэффициенты разложения новых базисных векторов 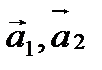по старому базису 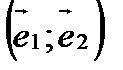образуют столбцы матрицы перехода ).

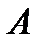Найдём 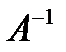. Напомним формулы, для нахождения обратной матрицы: 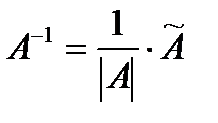, 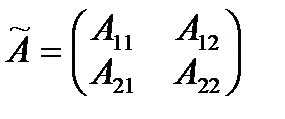. Вычислим

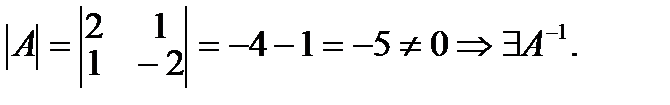
Таким образом, 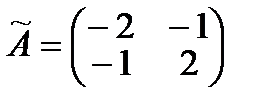, значит, .

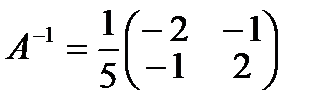Находим координаты вектора 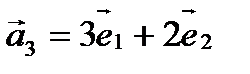в базисе :

.

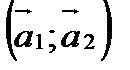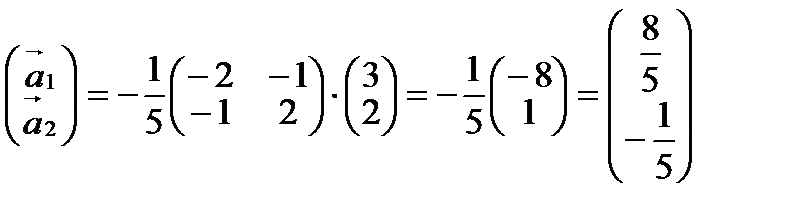Ответ: .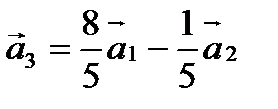

Линейные операторы

Определение.Пусть 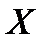и 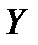два линейных пространства.

Линейным оператором, действующим из 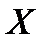в 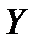называется отображение 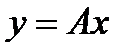, , 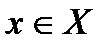, 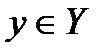которое удовлетворяет следующим условиям:

1. 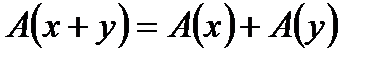- свойство аддитивности оператора;

2. 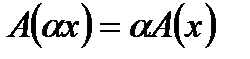- свойство однородности оператора.

Пример 52.Проверить линейность оператора