Лекция 5. Решение уравнений векторного поля
Метод потенциалов
Рассмотрим вопрос о единственности решения уравнений векторного поля. Запишем эти уравнения в виде системы:
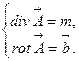 (5.1)
(5.1)
Представим поле 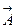 в виде суммы двух полей:
в виде суммы двух полей: 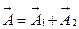 ,удовлетворяющих следующим уравнениям.
,удовлетворяющих следующим уравнениям.
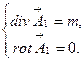
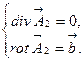 (5.2)
(5.2)
Из этих уравнений видно, что 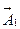 порождается источниками (стоками), т.к.
порождается источниками (стоками), т.к. 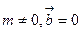 и является чисто источниковым, а чисто вихревым, т.к. причинами его возникновения являются вихри:
и является чисто источниковым, а чисто вихревым, т.к. причинами его возникновения являются вихри: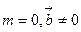 . Рассмотрим сначала поле
. Рассмотрим сначала поле 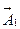 . Из таб.1. видно, что если вектор
. Из таб.1. видно, что если вектор 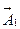 представить в виде:
представить в виде: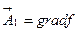 , то он будет решением второго уравнения, т.к.
, то он будет решением второго уравнения, т.к.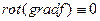 и совместным решением всей системы при условии, что
и совместным решением всей системы при условии, что 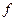 удовлетворяет следующему уравнению: или, окончательно,
удовлетворяет следующему уравнению: или, окончательно,
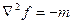 (5.3)
(5.3)
Уравнение (5.4) хорошо известно и носит название уравнения Пуассона. Имеется доказательство единственности его решения и известны методы его получения. Таким образом, вопрос о нахождении вектора 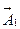 мы свели к решению дифференциального уравнения второго порядка в частных производных. Это большая самостоятельная задача, с которой читатель познакомится в курсе методов математической физики.
мы свели к решению дифференциального уравнения второго порядка в частных производных. Это большая самостоятельная задача, с которой читатель познакомится в курсе методов математической физики.
Рассмотрим вторую систему уравнений (5.2). Из первого уравнения этой системы и таб.1. следует, что вектор 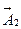 всегда можно представить в виде:
всегда можно представить в виде: 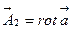 (5.4)
(5.4)
т.к. в этом случае он является решением первого уравнения, поскольку 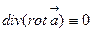 . Для совместного решения системы необходимо, чтобы вектор
. Для совместного решения системы необходимо, чтобы вектор 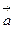 удовлетворял уравнению
удовлетворял уравнению
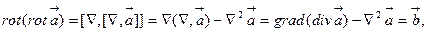 (5.5)
(5.5)
Очевидно, что уравнение (5.6) не проще исходной системы уравнений, т.к. не удалось "расщепить" его на три скалярных уравнения относительно компонент 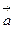 . Чтобы это осуществить, рассмотрим множество векторов
. Чтобы это осуществить, рассмотрим множество векторов 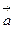 , преобразующихся по формуле
, преобразующихся по формуле 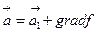 , (5.6)
, (5.6)
где 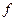 произвольная функция координат. Подставим (5.6) в (5.4) и воспользуемся таб.1.
произвольная функция координат. Подставим (5.6) в (5.4) и воспользуемся таб.1.
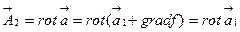 , т.е. вихревое поле
, т.е. вихревое поле 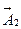 не зависит от добавки градиента произвольной функции к вектор-потенциалу
не зависит от добавки градиента произвольной функции к вектор-потенциалу 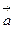 . Другими словами, поле
. Другими словами, поле 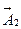 допускает преобразование (5.6). Это свойство вихревого поля называется градиентной инвариантностью. Оно позволяет осуществить калибровку (отбор) вектор-потенциалов
допускает преобразование (5.6). Это свойство вихревого поля называется градиентной инвариантностью. Оно позволяет осуществить калибровку (отбор) вектор-потенциалов 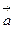 так, чтобы упростить уравнение (5.5). Например, Лоренц предложил следующее условие калибровки:
так, чтобы упростить уравнение (5.5). Например, Лоренц предложил следующее условие калибровки: 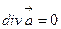 .В этом случае уравнение (5.5) принимает вид:
.В этом случае уравнение (5.5) принимает вид: 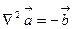 . (5.7)
. (5.7)
Не трудно сообразить, что (5.7) представляет собой систему трех скалярных уравнений типа (5.3) относительно проекций вектора 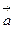 , т.е. задачу об отыскании поля
, т.е. задачу об отыскании поля 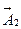 мы снова свели к проблеме решения уравнения Пуассона.
мы снова свели к проблеме решения уравнения Пуассона.
Таким образом, полное поле 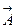 теперь можно выразить с помощью потенциалов
теперь можно выразить с помощью потенциалов 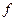 и
и 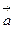 , которые, в свою очередь, могут быть получены из решения уравнений Пуассона (5.3), (5.7) и калибровки Лоренца:
, которые, в свою очередь, могут быть получены из решения уравнений Пуассона (5.3), (5.7) и калибровки Лоренца:
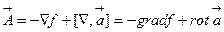 (5.8)
(5.8)
Формулы Грина
Рассмотрим формулу Остроградского-Гаусса: 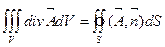 . (5.9)
. (5.9)
Допустим, что вектор 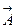 можно представить в виде:
можно представить в виде: 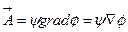 , где
, где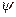 и
и 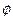 - произвольные функции координат непрерывные вместе со своими первыми производными внутри области и на поверхности и
- произвольные функции координат непрерывные вместе со своими первыми производными внутри области и на поверхности и
имеющие непрерывные вторые производные внутри области. Вычислим
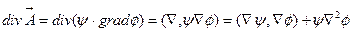 ,
,
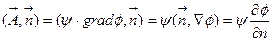
где 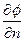 -производная по направлению
-производная по направлению 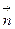 . Подставив эти вычисления в (5.9), получим
. Подставив эти вычисления в (5.9), получим
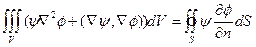 (5.10)
(5.10)
несимметричную формулу Грина, которая часто используется в теоретических разделах физики. Легко симметризовать эту формулу, поменяв местами функции 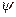 и
и 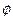 в формуле (5.10):
в формуле (5.10):
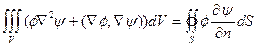 (5.11)
(5.11)
Вычитая равенство (5.11) с (5.10), получим симметричную формулу Грина:
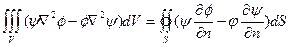 (5.12)
(5.12)
Упражнение 5
1. Найти потенциалы следующих векторных полей:
1) 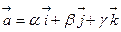 , где
, где 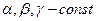 ,
,
2) 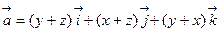 ,
,
3) 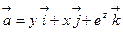 ,
,
4) 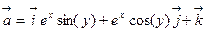 ,
,
2. Найти векторные потенциалы соленоидальных полей:
1) 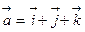 ,
,
2) 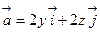 ,
,
3) 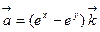 ,
,
4) 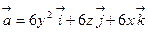 ,
,
5) 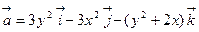 ,
,
6) 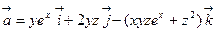 .
.
Дата добавления: 2016-10-17; просмотров: 1148;
