Второе уравнение векторного поля

Для лучшего понимания дальнейшей теории полезно рассмотреть физический пример. Пусть по тонкому прямолинейному проводнику течет постоянный ток 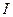. Известно, что вокруг этого проводника существует магнитное поле 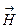, силовые линии которого представляют собой концентрические окружности. Вычислим циркуляцию поля 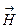по замкнутому контуру L, выбрав для простоты в качестве L одну из векторных линий: 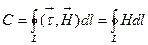.Здесь мы воспользовались тем, что 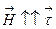и .

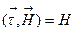С другой стороны поле 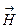для прямого проводника задается формулой Ампера [4] .

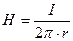После подстановки получим 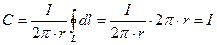. Несмотря на простоту полученного результата, в нем заложен глубокий физический смысл. С одной стороны, циркуляция вектора зависит от распределения поля в обл. D на кривой L, с другой стороны, мы показали на примере,

что она равна полному току пересекающему площадку, ограниченную контуром L. Из физики известно, что ток следует отождествить с суммарной мощностью вихрей. Таким образом, уравнение 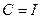дает интегральную связь поля с вихрями. Этот частный вывод обобщим на все случаи жизни, высказав следующее предположение.

Циркуляция векторного поля 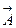по замкнутому контуру L всегда пропорциональна (в соответствующей системе единиц равна) проекции на 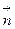интегральной (полной) мощности вихрей, пересекающих поверхность, ограниченную контуром L.

Запишем это утверждение в виде следующего уравнения: 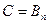. (3.7)

Здесь 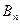- число, характеризующее полную мощность вихрей, пересекающих площадку 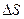в направлении 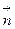, например, для электромагнитного поля 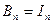- проекция полного тока, пересекающего поверхность, на нормаль к этой поверхности.

Воспользуемся уравнением (3.6) и определением 3.3. для построения еще одного уравнения векторного поля: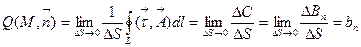

где 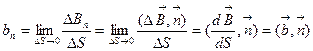- поверхностная плотность мощности вихря в точке M по направлению нормали 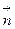. В таком случае из уравнения (3.7) следует

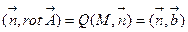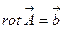или (3.8)

Это и есть искомое второе уравнение векторного поля в дифференциальной форме. Прежде чем его анализировать, получим ряд полезных соотношений. Для этого выберем произвольную кусочно-гладкую незамкнутую поверхность S и проинтегрируем по ней уравнение (3.8):

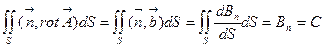
или, воспользовавшись (3.4) 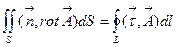(3.9)

Формула (3.9) называется вторым уравнением векторного поля в интегральной форме, в математике она известна как формула Остроградского-Стокса. И еще, рассмотрим произвольную кусочно-гладкую замкнутую поверхность S и будем стягивать ее в точку M. Вычислим приращение 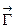(3.1) при изменении поверхности S:

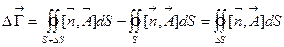. Объемная плотность приращения этого вектора равна

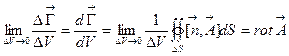, или 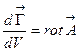(3.10)

Таким образом, мы еще раз убедились в том, что ротор вектора представляет собой некоторую производную от вектора по объему. Интегрируя последнее равенство по произвольному объему V, получим формулу Остроградского-Гаусса, которая потребуется нам при выводе выражения ротора в ДСК: 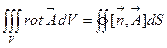(3.11)

Подведем некоторый итог. Мы ставили перед собой цель построить уравнения, позволяющие однозначно связать векторное поле со своими источниками, стоками и вихрями. Нам удалось это сделать с помощью уравнений (2.12) и (3.8). Теперь можно снова вернуться к проблеме определения векторного поля. Для ее решения необходимо вычислить вектор 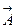, или три его проекции 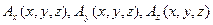из четырех уравнений (2.12) и (3.8). Таким образом, количество уравнений больше числа неизвестных, что делает обратную задачу теории поля переопределенной. К этому вопросу мы еще вернемся, а сейчас рассмотрим операцию ротора в ДСК.