Вихревые векторные поля

Прежде, чем приступить к построению второго уравнения векторного поля, необходимо более детально разобраться в существе проблемы. Почему возникла недоопределенность обратной задачи? Чтобы ответить на этот вопрос, вспомним, как строилось первое уравнение (2.14). Исходным было понятие потока вектора через замкнутую поверхность. 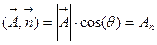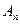Для этого в каждой точке поверхности строилось скалярное произведение вида , где - ортогональная проекция вектора 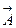к поверхности S. Из линейной алгебры известно, что любой вектор, заданный на поверхности, всегда можно разложить на ортогональную 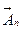и тангенциальную 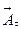компоненты согласно правилу параллелограмма: 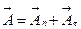. До сих пор мы рассматривали только нормальную компоненту и полностью игнорировали тангенциальную. Это привело к тому, что вектор 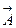из полученного уравнения однозначно не определяется. Таким образом, чтобы разрешить обратную задачу теории поля, необходимо, образно говоря, задействовать тангенциальную проекцию вектора .

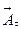Так выглядит проблема с математической точки зрения. Посмотрим на нее с точки зрения физики. Все наши прежние рассуждения будут иметь смысл, если в области D существуют точки, где векторные линии исчезают или возникают, т.е. имеются источники или стоки поля. Поток вектора 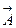через замкнутую поверхность в этом случае не равен нулю и уравнение (2.12) не вырождается в нулевое тождество.

Предположим, что в природе существуют поля, имеющие замкнутые векторные линии. В этом случае предыдущая теория перестает работать, т.к. уравнения (2.9) и (2.12) вырождаются в нулевое тождества. Теперь становится понятной возникшая проблема с решением обратной задачи. До сих пор мы рассматривали векторные поля чисто источниковые и не учитывали возможность существования векторных полей с замкнутыми векторными линиями. О том, что такие поля существуют, нам говорит опыт. В частности, хорошо известно, что вокруг прямолинейного проводника с током всегда можно обнаружить магнитное поле, векторные линии которого - концентрические окружности. Эти предварительные рассуждения подсказывают нам дальнейший путь построения уравнений векторного поля.

ОПРЕДЕЛЕНИЕ 3.1. Векторные поля с замкнутыми векторными линияминазываются вихревыми (соленоидальными).

ОПРЕДЕЛЕНИЕ 3.2.Причины, порождающие вихревые поля называются вихрями.