Вычисление дивергенции в ДСК
Введем ДСК и получим выражение дивергенции в этой системе координат. Из определения 2.5 следует, что результат вычисления не должен зависеть от выбора первоначальной поверхности 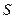 , поэтому в качестве замкнутой поверхности удобно выбрать достаточно малый (в пределе бесконечно малый) прямоугольный параллелепипед (см. рис. 4.). Разобьем полную поверхность
, поэтому в качестве замкнутой поверхности удобно выбрать достаточно малый (в пределе бесконечно малый) прямоугольный параллелепипед (см. рис. 4.). Разобьем полную поверхность 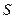 на совокупность граней
на совокупность граней 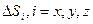 и обозначим противоположные грани штрихом, тогда
и обозначим противоположные грани штрихом, тогда
Рис. 1.3. Вычисление дивергенции в ДСК
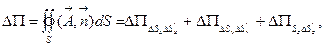
где 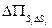 - поток вектора
- поток вектора 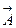 соответствующие противоположные грани параллелепипеда. Вычислим, например,
соответствующие противоположные грани параллелепипеда. Вычислим, например, 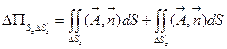 .
.
Очевидно, что на 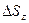
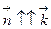 и
и 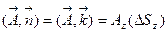 . На
. На 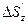
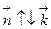 и
и
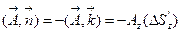 . Интегралы по поверхностям вычислим по теореме Лагранжа о среднем:
. Интегралы по поверхностям вычислим по теореме Лагранжа о среднем: 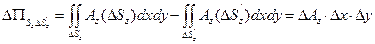
где 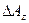 -- приращение вертикальной компоненты поля
-- приращение вертикальной компоненты поля 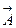 при переходе от грани
при переходе от грани 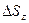 к противоположной -
к противоположной - 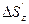 . Аналогичные вычисления справедливы и для оставшихся граней:
. Аналогичные вычисления справедливы и для оставшихся граней:
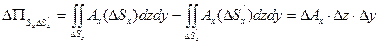
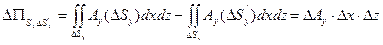
Полный поток векторного поля через замкнутую поверхность равен сумме
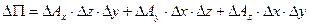
Подставим это выражение в формулу (2.10) и устремим 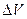 к нулю:
к нулю:
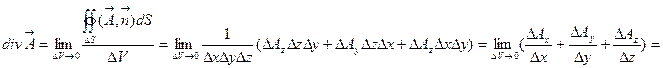
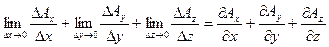 . Окончательно можно записать:
. Окончательно можно записать:
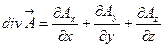 (2.14)
(2.14)
Формула (2.14) задает выражение дивергенции в ДСК, вид которого зависит от выбора системы координат, в то время как определение (2.10) является инвариантным.
Подведем некоторый итог. С одной стороны, поток вектора через замкнутую поверхность (2.4) зависит от распределения поля по поверхности и равен разности количества выходящих и входящих векторных линий. С другой стороны, эта разность пропорциональна суммарной мощности источников и стоков, заключенных внутри поверхности. Это позволило записать интегральное уравнение, связывающее источники с полем. Чтобы получить дифференциальное уравнение, потребовалось понятие дивергенции (2.10). Таким образом, мы имеем первое уравнение векторного поля в интегральной (2.9) и дифференциальной (2.12) формах. С помощью этих уравнений можно решат как прямую (вычисление функции 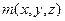 , описывающей распределение источников и стоков по заданному распределению поля
, описывающей распределение источников и стоков по заданному распределению поля 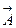 в обл. D), так и обратную задачу (определение поля
в обл. D), так и обратную задачу (определение поля 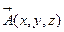 по известной плотности мощности источников и стоков
по известной плотности мощности источников и стоков 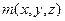 ). Обратная задача теории поля значительно сложней прямой, так как для ее решения необходимо рассматривать уравнения в частных производных. И все же, основная проблема не в этом. Посмотрим на уравнение (2.12) более внимательно. В ДСК оно имеет вид:
). Обратная задача теории поля значительно сложней прямой, так как для ее решения необходимо рассматривать уравнения в частных производных. И все же, основная проблема не в этом. Посмотрим на уравнение (2.12) более внимательно. В ДСК оно имеет вид:
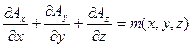 (2.15)
(2.15)
Мы имеем одно скалярное уравнение, в то время как неизвестных функций три: 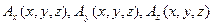 т.е. количество неизвестных больше числа уравнений. Таким образом, мы приходим к неутешительному выводу о том, что обратная задача теории поля при наличии только одного уравнения (2.15), в общем случае, не имеет однозначного решения. Для нас это означает, что нам рано останавливаться на достигнутом. Необходимо строить еще дополнительные уравнения, которые бы связали поле с порождающими его причинами. Это и будет темой следующей лекции.
т.е. количество неизвестных больше числа уравнений. Таким образом, мы приходим к неутешительному выводу о том, что обратная задача теории поля при наличии только одного уравнения (2.15), в общем случае, не имеет однозначного решения. Для нас это означает, что нам рано останавливаться на достигнутом. Необходимо строить еще дополнительные уравнения, которые бы связали поле с порождающими его причинами. Это и будет темой следующей лекции.
Упражнение 2
1) Построить векторные линии следующих векторных полей:
a) 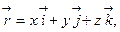
b) 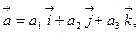 где
где 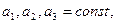
c) 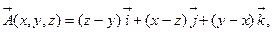
d) 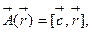 где
где 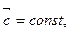
e) 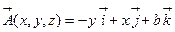 , где
, где 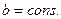
2) Построить векторные линии магнитного поля бесконечного проводника с током, заданного формулой: 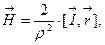 где
где 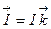 - вектор тока,
- вектор тока, 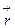 - радиус-вектор точки
- радиус-вектор точки 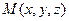 ,
,
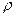 -расстояния от оси проводника до точки
-расстояния от оси проводника до точки 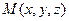 .
.
3) Вычислить поток векторного поля 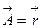 - радиус-вектор через прямой круговой цилиндр высотой h, радиусом основания R и осью симметрии Oz.
- радиус-вектор через прямой круговой цилиндр высотой h, радиусом основания R и осью симметрии Oz.
4) Найти поток векторного поля 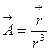 через сферу радиуса R с центром в начале координат.
через сферу радиуса R с центром в начале координат.
5) Используя теорему Остроградского - Гаусса, вычислить потоки векторных полей через указанную замкнутую поверхность S.
a) 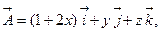
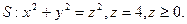
b) 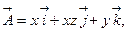
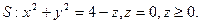
c) 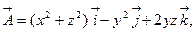
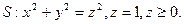
6) Найти дивергенцию следующих векторных полей в ДСК:
a) 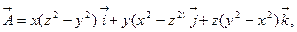
b) 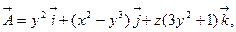
c) 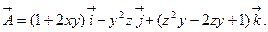 $
$
7) Вычислить дивергенцию следующих векторных полей, используя ее свойства:
a) 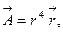
b) 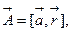
c) 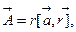
d) 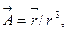
e) 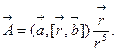
Лекция 3
Дата добавления: 2016-10-17; просмотров: 1500;
