Ротор векторного поля

Рассмотрим снова замкнутую кусочно-гладкую поверхность 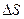. В каждой точке этой поверхности восстановим внешнюю нормаль и построим векторное произведение 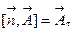. Из определения векторного произведения следует, что вектор 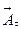совпадает с касательным (тангенциальным) вектором к поверхности 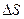. По аналогии с потоком вектора вычислим поверхностный интеграл следующего вида:

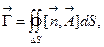(3.1)

и предположим, что он дает информацию о наличии внутри поверхности 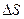причин, порождающих векторные поля с замкнутыми векторными линиями. В дальнейшем, чтобы использовать общепринятую в теории поля терминологию, будем называть эти причины вихрями. К сожалению, в литературе нет общепринятого определения вихря и даже трактовка этого понятия у некоторых авторов различна. Мы будем понимать под вихрями причину, другими словами, особые точки в области D, в которых находятся "источники", создающие поля с замкнутыми векторными линиями. Такие векторные поля называются вихревыми. Следует иметь в виду, что в данном контексте слово "источники" имеет совсем иной смысл, чем в определении 2.3. В качестве примера можно рассмотреть электромагнитное поле, где источниками и стоками являются положительные и отрицательные заряды, а вихрями - электрические токи.

Предположим, что интеграл (3.1) дает интегральную характеристику вихрей внутри поверхности 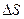. Чтобы получить дифференциальную (точечную) связь между полем и его вихрями, снова воспользуемся предельным переходом и введем следующее понятие.

ОПРЕДЕЛЕНИЕ 3.3. Ротором вектора 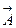называется предел следующего вида:

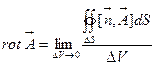(3.2)

если он существует и не зависит от выбора первоначальной поверхности 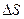и способа стремления 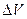к нулю. Из этого определения видно, что 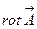есть некоторая дифференциальная

операция от вектора. Вид этой операции в некоторой системе координат нам предстоит еще определить, а сейчас попытаемся выяснить ее физический смысл. Для этого рассмотрим в качестве замкнутой поверхности малый круговой цилиндр высотой h и полной поверхностью 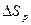(см. рис.5).

Рис. 5 Вычисление проекции ротора на нормаль

В точке M построим 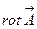и нормаль 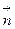. Вычислим скалярное произведение 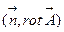в точке M:

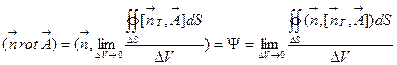
Здесь 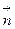- фиксированная нормаль в точке M, 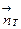-- текущая нормаль, заданная в точках на поверхности цилиндра. Полную поверхность 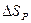разобьем на боковую 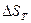, верхнее 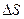и нижнее 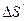основание. Тогда 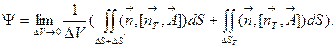На верхнем и нижнем основаниях нормал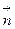и и 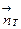коллинеарны, следовательно, смешанное произведение 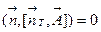. Таким образом, остается вычислить только интеграл по боковой поверхности

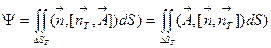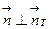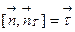цилиндра : . На боковой поверхности, и , где 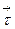- вектор касательный к боковой поверхности цилиндра. При 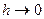он становится касательным к окружности L. В таком случае имеем: 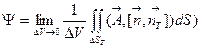. Объем цилиндра равен 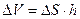, элемент боковой поверхности 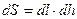- элемент дуги окружности L. Из определения 3.1. следует, что предел (3.2) не зависит от способа стремления 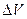к нулю, поэтому устремим сначала 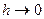, а затем 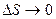в точку M. Тогда,

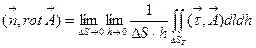.Интеграл по поверхности разобьем на повторные интегралы по L и по h: 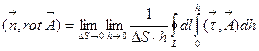.Интеграл по h вычислим, воспользовавшись теоремой Лагранжа о среднем: 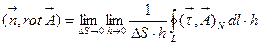.Здесь скалярное произведение вычисляется в некоторой точке 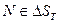. В пределе при 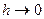точка N попадает на контур L. Окончательно, 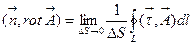(3.3)

Если точку M рассматривать как произвольную точку обл. D, то предел (3.3) можно получить в любой точке, где задано поле 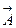. Интеграл в правой части выражения (3.3) играет важную роль в теории поля и называется циркуляцией вектора 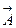по замкнутому контуру L.

ОПРЕДЕЛЕНИЕ 3.4. Циркуляцией векторного поля 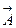по замкнутому контуру L называется криволинейный интеграл вида 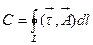. (3.4)

Очевидно, что предел (3.3) есть циркуляция векторного поля, приходящаяся на единицу площади, т.е. поверхностная плотность циркуляции.

ОПРЕДЕЛЕНИЕ 3.3. Поверхностной плотностью циркуляции вектора в точке M называется предел следующего вида 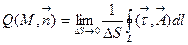(3.5)

если он существует и не зависит от выбора первоначальной поверхности и способа стягивания ее в точку.

Если внимательно проследить за выводом уравнения (3.3), то становится ясно, что плотность циркуляции является функцией точки M и зависит от ориентации нормали 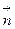в этой точке к первоначально выбранной поверхности 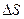. Уравнение (3.3), с учетом уравнения (3.5), принимает следующий вид 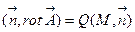. (3.6)