Дивергенция векторного поля

Пусть задана кусочно-гладкая замкнутая поверхность 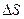(см. рис. 3), ограничивающая объем 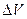. Вычислим, отнесенный к единице объема, поток векторного поля через эту поверхность. Рассмотрим предел следующего отношения:

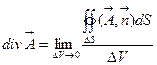(2.10)

ОПРЕДЕЛЕНИЕ 2.6. Дивергенцией (расходимостью) вектора 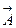в точке 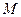называется предел отношения (2.10), если он существует и не зависит от выбора первоначальной поверхности и способа стягивания 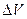к нулю.

Необходимо сделать следующие замечания [3]:

1) Дивергенция является дифференциальной операцией и представляет из себя производную от потока вектора по объему.

(2.11)

2) Выражение дивергенции не должно зависеть от выбора первоначальной поверхности и способа стягивания ее в точку.

3) Дивергенция определена в любой точке области D, где задано поле, независимо от выбора системы координат.

Выясним физический смысл дивергенции. Для этого вернемся к уравнению (2.9) и замечанию 1, из которых следует:

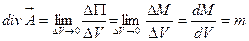, или окончательно

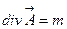(2.12)

где 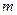-- объемная плотность мощности источников и стоков поля 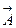в точке 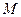. Отсюда следует:

1) Если 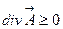в некоторой точке, то в этой точке имеется источник.

2) Если 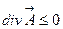в некоторой точке, то в этой точке имеется сток.

3) Если 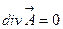в некоторой точке, то в этой точке нет ни источника, ни стока.

Уравнение (2.11) называется первым уравнением векторного поля в дифференциальной форме, в то время как уравнение (2.9) -- первым уравнением векторного поля в интегральной форме. Уравнение (2.9) легко представить в форме теоремы Остроградского-Гаусса, проинтегрировав равенство (2.12) по произвольному объему V:

.

Таким образом

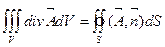(2.13)