Размерность и базис векторного пространства

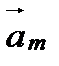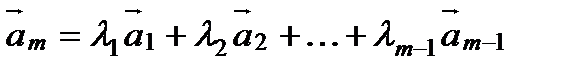Определение.Вектор называется линейной комбинацией векторов векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа: (1)

где - какие-либо действительные числа.

Определение.Векторы 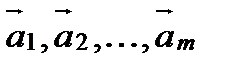называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно , т.е. .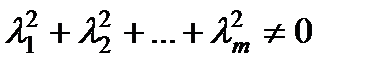

Если же только при 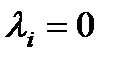выполняется , то векторы называются линейно независимыми.

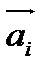Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Любые 4 вектора в трехмерном пространстве линейно зависимы.

Пример 49.Выяснить являются ли векторы линейно зависимыми или линейно независимыми: , , .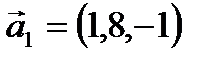

Решение:

векторы являются линейно зависимыми, если существуют такие значения , , , из которых хотя бы одно отлично от нуля, что будет выполняться верное равенство:

.

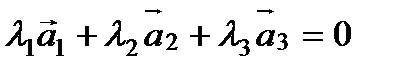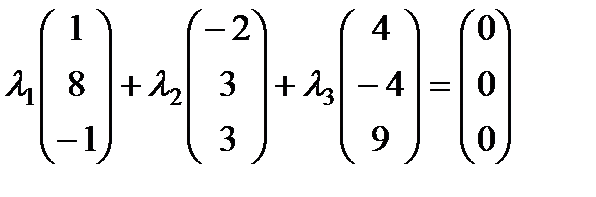
Таким образом, задача сводится к решению системы:

Вычислим определитель основной матрицы.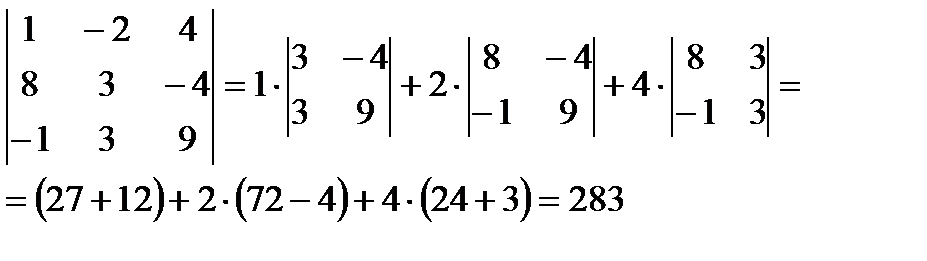

Определитель отличен от нуля, система определенная.

Решим полученную систему методом Гаусса (приведем её к ступенчатому виду):

~ ~

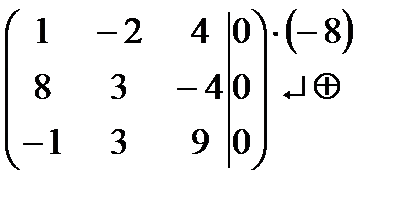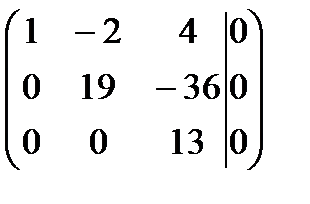
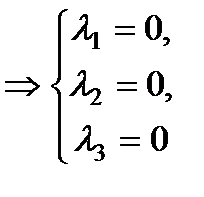
Ранг матрицы системы равен числу переменных , отсюда следует, данная система имеет единственное нулевое решение 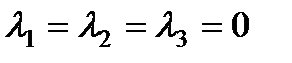, значит система векторов - линейно независима.

Определение. Линейное пространство R называется 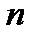- мернымесли в нем существует линейно независимых векторов, а любые из векторов уже являются зависимыми. Другими словами. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Число называется размерностью пространства R и обозначается dim(R).