Градиент скалярного поля

Преобразуем выражение (1.6) таким образом, чтобы его вид не зависел от выбора системы координат. Для этого введем специальный вектор, имеющий в ДСК следующее представление:

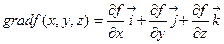(1.7)

( -- читается "градиент"). Вычислим скалярное произведение векторов (1.4) и (1.7).

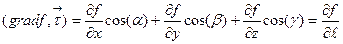Правая часть полученного выражения представляет из себя производную по направлению в ДСК (см. фор.(1.6)), тогда в любой система координат имеет место равенство:

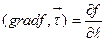(1.8)

Равенство (1.7) позволяет дать физическое толкование и служит определение градиента скалярного поля. В самом деле, выберем направление 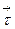так, чтобы оно совпадало с вектором 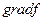и распишем скалярное произведение (1.8) по определению:

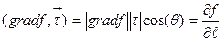где 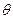-- угол между вектором 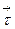и градиентом. Т.к. в нашем случае 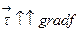то 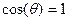,производная по направлению достигает максимального значения и равна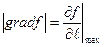

ОПРЕДЕЛЕНИЕ 1.4. Градиентом скалярного поля 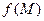называется вектор, который указывает направление наибольшей скорости роста поля и модуль которого в данной точке равен максимальной производной по направлению.

Из определения 1.4. следуют некоторые свойства градиента:

1. Рассмотрим ПРУ для поля 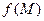(см.1.1) и вычислим производную по касательному направлению к ПРУ. С одной стороны, эта производная равна нулю, с другой –

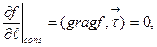если 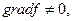то 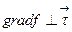. Таким образом, градиент скалярного поля (если он не равен нулю) всегда ортогонален ПРУ.

2. Докажем свойство линейности для операции градиент скалярного поля. Пусть поле 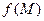имеет вид 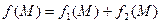, тогда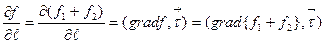

Используя свойство линейности для производной, получим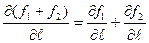

Сумму производных по направлению распишем по формуле (1.8), тогда

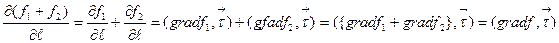, окончательно

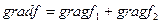.Градиент суммы скалярных полей равен сумме градиентов.Не сложно доказать, что для вычисления градиента необходимо пользоваться теми же правилам что и при вычислении производной.

Упражнение 1

1) Построить поверхности равного уровня следующих скалярных полей.

a)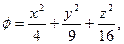

b)

c)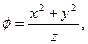

d)

e)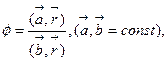

f)

2) Построить линии равного уровня следующих плоских скалярных полей.

a)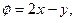

b)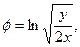

c)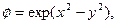

3) Найти производные для следующих скалярных полей в точке 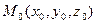по направлению к точке .

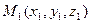a)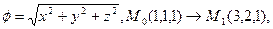

b)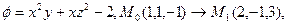

c)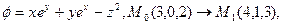

4) Найти производную скалярного поля 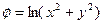в точке 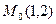параболы по направлению этой кривой.

5) Найти производную скалярного поля в точке 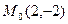на кривой 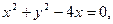двигаясь против часовой стрелки.

6) Найти производную скалярного поля 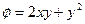в точке 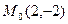на линии 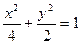по направлению внешней нормали к линии в этой точке.

7) Найти производную скалярного поля 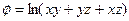в точке 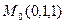по направлению окружности: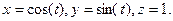

8) Вычислить производную скалярного поля 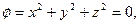в точке 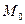соответствующей значению параметра 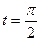по направлению винтовой линии

9) Найти градиенты следующих скалярных полей в точке :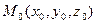

a)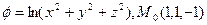

b)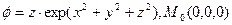

c)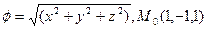

10) Найти градиенты следующих скалярных полей, есл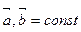и и

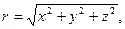
a)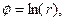

b)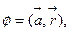

c)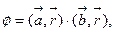

d)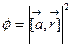

11) Найти направление и величину наибольшего изменения для следующих скалярных полей в заданных точках :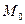

a)

b)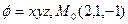

c)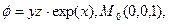

d)