Производная по направлению. Основные понятия и определения

Скалярное поле

Основные понятия и определения

В физике и математике ( и других сферах человеческой деятельности ) приходится иметь дело с величинами двух родов: одни из них можно задать числом, другие связаны с понятием о направлении в пространстве и для своего задания требуют уже несколько чисел ( три и больше). Примером первых могут служить такие физические величины, как температура, плотность вещества, масса тела, давление в жидкости и др. Примером вторых - скорость, импульс тела, характеристики электромагнитного и гравитационного полей [1].

Если эти величины меняются в пространстве и времени, то их объединяют общим названием - поле ( скалярное, векторное, тензорное).

Рассмотрим наиболее простое понятие скалярного поля. Дадим строгое математическое определение.

ОПРЕДЕЛЕНИЕ 1.1. Если в некоторой области пространства D, каждой точке M единственным образом ставится в соответствие число 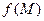, то в области D задано скалярное поле.

Пусть в обл. D введена Декартова Система Координат (ДСК), тогда точку M можно задать с помощью декартовых переменных 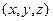, а скалярное поле 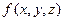рассматривать как функцию координат.

Реальные скалярные поля часто обладают определенной симметрией, знание которой значительно облегчает изучение их. Для обнаружения этой симметрии вводится понятие Поверхности Равного Уровня (ПРУ).

ОПРЕДЕЛЕНИЕ 1.2. Поверхностью Равного Уровня (ПРУ) скалярного поля называется геометрическое место точек, в которых

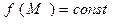(1.1)

т.е. поверхность, где поле принимает постоянные значения. Задавая различные значения const мы построим семейство ПРУ. Из определения 1.1 следует, что ПРУ не могут пересекаться, в противном случае в точке пересечения однозначность поля нарушается. Однако в обл. D могут существовать особые точки, в которых поле 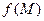невозможно задать однозначно, поэтому более точно утверждение: во всех точках обл. D, где поле 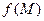задано однозначно, ПРУ не пересекаются. Физически это означает, что в точках, где поле не определено, расположены источники этого поля (причины, которые его порождают) и основная задача состоит в том, чтобы найти связь между полем и его источниками (записать уравнение поля и решить его). Эта задача выходит за рамки нашего курса. Детально она будет изучена в разделах математической физики.

Производная по направлению

Нам сейчас необходимо научиться исследовать свойства скалярных полей по заранее выбранным направлениям в пространстве, например, следующим образом.

Пусть требуется установить, как быстро изменяется функция 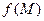вдоль некоторой линии L (см. рис. 1). Для этого в двух точках M , M 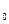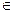L вычислим значение 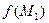) и 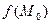и составим предел следующего отношения:

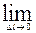
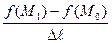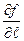= (1.2)

Здесь 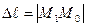- расстояния между рассматриваемыми точками.

ОПРЕДЕЛЕНИЕ 1.3. Производной скалярного поля 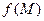в точке по направлению кривой L (сокращенно - производная по направлению), называется предел (1.2), если он существует и не зависит от способа стремления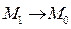

Из определения 1.3 следует, что производная по направлению (1.2) является функцией не только предельной точки M, но и вектора 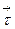, задающего направление на кривой L (см. рис. 1.).

рис. 1.1

Определение производной по направлению.

Рассмотрим кривую L и вектор 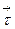в ДСК. Линию L зададим в параметрической форме:

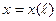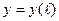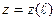, , (1.3)

а вектор 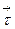- стандартным разложением: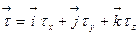

Поскольку 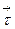- единичный вектор, то.

, ,

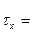
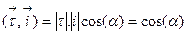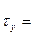
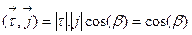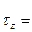
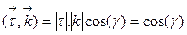
где 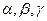-- углы между ортами ДСК и вектором 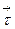. Окончательно 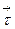в ДСК будет иметь вид: 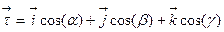(1.4)

Если учесть уравнения (1.3), то скалярное поле на кривой L можно рассматривать как сложную функцию параметра 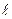: 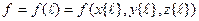.Воспользуемся формулой вычисления сложной производной: 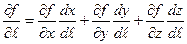(1.5)

Из рис. 1. видно, что, например,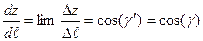 .Аналогично для остальных координат: ,

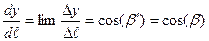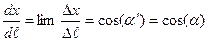
Подставим найденные значения производных в (1.4а) и получим выражение производной по направлению в ДСК:

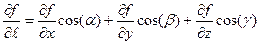1.6)