Поток векторного поля

Для полного геометрического описания векторных полей необходимо доопределить понятие векторной линии таким образом, чтобы оно отражало не только пространственную ориентацию поля, но и распределения его по величине в обл. D.

Рассмотрим в обл. D малую площадку 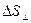, перпендикулярную к векторной линии. Обозначим 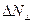число векторных линий пересекающих эту площадку.

ОПРЕДЕЛЕНИЕ 2.4. Плотностью векторных линий в обл. D называется предел следующего отношения:

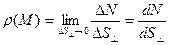(2.3)

Предположим, что плотность векторных линий прямо пропорциональна величине поля :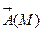

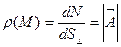(2.4)

Правомерность такого предположения обосновывается тем, что чем ближе расположена точка, в которой рассматривается поле, к источнику, тем данное поле больше по величине и тем плотнее его векторные линии. Если рассматривать произвольную площадку 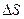и ввести нормаль к ней, то, как видно из рис.2а,

Рис. 2а. К определению потока вектора через поверхность

, где 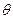-- угол между векторам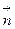и и 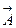. Тогда из (2.4) имеем:

(2.5)

(Здесь необходимо брать знак "+", если угол 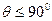и знак "-", если 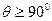.) Очевидно, что равно числу векторных линий, пересекающих бесконечно малую площадку 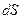. Если рассмотреть в обл. D произвольную кусочно-гладкую поверхность S, то число векторных линий пересекающих эту поверхность будет равно:

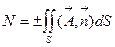(2.6)

Рассмотрим в обл. D кусочно-гладкую замкнутую поверхность S (см. рис. 2b) и вычислим интеграл следующего вида:

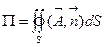(2.7)

ОПРЕДЕЛЕНИЕ 2.5. Потоком вектора 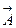через замкнутую поверхность S называется поверхностный интеграл вида (2.7).

Выясним физический смысл введенного понятия. Для этого замкнутую поверхность S разобьем на множество точек 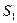, в которых векторные линии выходят из поверхности и множество точек , в которых векторные линии входят. Тогда легко показать, что

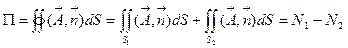(2.8)

где -- число выходящих, -- число входящих векторных линий. Очевидно, что возможны следующие случаи:

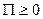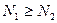1) Если или , т.е. число выходящих линий больше числа входящих, то внутри замкнутой поверхности имеются не скомпенсированные источники.

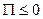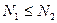2) Если или, т.е. число входящих линий больше числа выходящих, то внутри замкнутой поверхности имеются не скомпенсированные стоки.

3) Если 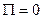или ,т.е. число входящих линий равно числу выходящих, то внутри поверхности отсутствуют источники и стоки, либо они полностью взаимно компенсируют друг друга.

Рассмотренные случаи позволяют сделать важный физический вывод - поток вектора через замкнутую поверхность дает интегральную (суммарную) характеристику наличия источников и стоков внутри этой поверхности. При соответствующем выборе этой характеристики можно предположить, что поток численно равен интегральной мощности источников и стоков:

(2.9).

где 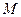-- физическая величина, характеризующая интегральную мощность источников и стоков в объеме 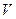. Физический смысл данного утверждения состоит в том, что таким образом удается связать величину , зависящую от распределения векторного поля в пространстве и величину 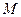, задающую суммарную мощность источников и стоков, т.е. найти интегральную связь между полем и его источниками и стоками.

Построенное уравнение (2.9) не является локальным, так как оно дает связь между полем и его источниками не в точке, а в некоторой области. Для получения точечной или, как обычно говорят, дифференциальной связи между полем и причинами его порождающими, необходимо ввести новое понятие.