Лекция 2 Векторное поле

Основные понятия и определения

Разнообразие физических полей не исчерпывается только скалярными полями. Можно привести множество примеров, когда числовая характеристика поля уже не достаточна для однозначного его определения. В частности, такие поля как электромагнитное, гравитационное и др. определяются не только числом, но и задается определенное направление в каждой точке пространства. Такие поля называются векторными. Дадим строгое математическое определение этому понятию.

ОПРЕДЕЛЕНИЕ 2.1. Если в некоторой области пространства D каждой точке M 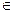D единственным образом сопоставляется вектор 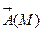, то в области D задано векторное поле.

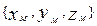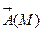Таким образом, физическое понятие векторного поля математически отображается однозначно на множество векторов. Если в области D построить систему координат (например, ДСК) и задать точку M ее координатами , то - вектор-функция в ДСК.

На практике конкретные физические поля во многих случаях обладают той или иной симметрией, для исследования которой удобно использовать геометрическое изображение векторного поля с помощью векторной линии.

ОПРЕДЕЛЕНИЕ 2.2. Векторной линией поля 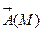называется кривая в обл. D, в каждой точке которой вектор поля 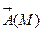направлен по касательной прямой к этой линии.

Запишем уравнение векторной линии. Пусть поле 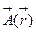задано в полярной системе координат.

Тогда векторную линию можно рассматривать как годограф радиус-вектора . Вычислим производную от радиус-вектора по параметру 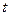. Этот вектор по определению будет касательным к годографу и, следовательно, коллинеарен вектору 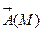. Из условия колинеарности имеем:

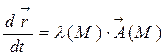(2.1.)

дифференциальное уравнение векторных линий в полярной системе координат. В ДСК векторному уравнению (2.1) будут соответствовать три скалярных уравнения:

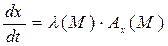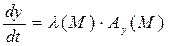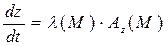, , (2.2.)

Решая эту систему обыкновенных дифференциальных уравнений, получим уравнения векторной линии в параметрической форме: .

Из определения векторного поля следует, что векторные линии не могут пересекаться в точках обл. D, где задано поле. В противном случае в точке пересечения векторной линии поле 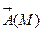будет задано неоднозначно. Однако в обл. D существуют особые точки, в которых векторные линии либо возникают, либо исчезают. В этих точках поле 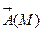становится неопределенным.

ОПРЕДЕЛЕНИЕ 2.3. Точечным источником (стоком) поля 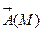называется особая точка обл. D, где возникает (исчезает) векторная линия.

Нетрудно сообразить, что источник (сток) произвольных размеров всегда можно представить как совокупность точечных.