ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ И ЕГО СВОЙСТВА
Если градиент функции 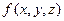 отличен от нуля в заданной точке, то значение производной по направлению по формуле (5.13 ) напрямую зависит от косинуса угла
отличен от нуля в заданной точке, то значение производной по направлению по формуле (5.13 ) напрямую зависит от косинуса угла  .
.
Ясно, что наибольшее значение производной по направлению достигается при 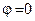 , когда направлением дифференцирования выбрано направление
, когда направлением дифференцирования выбрано направление 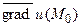 . Используя это соображение, можно сформулировать экстремальные свойства градиента.
. Используя это соображение, можно сформулировать экстремальные свойства градиента.
1. В точке 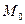 наибольшее значение производной по направлению
наибольшее значение производной по направлению 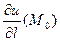 равно модулю градиента:
равно модулю градиента: 
где 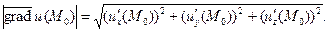
2. В точке 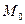 градиент определяет направление наибольшего роста функции:
градиент определяет направление наибольшего роста функции:
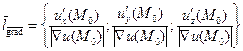 .
.
Здесь для сокращения записи использовано второе обозначение градиента: 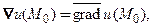
Заметим, что для функции двух переменных в приведенных формулах нужно исключить третьи компоненты; для функций четырех и большего числа переменных наоборот нужно добавить компоненты.
Пример 4. Найти направление наибольшего роста функции 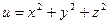 в точке
в точке  Вычислить производную заданной функции в этом направлении в точке
Вычислить производную заданной функции в этом направлении в точке 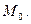
□ Используем экстремальные свойства градиента. Направление наибольшего роста
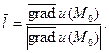
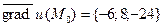 (см. пример 1).
(см. пример 1).
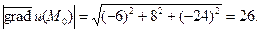
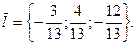
Производная по направлению 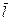 равна 26:
равна 26:
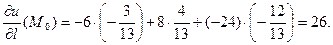 ■
■
Дата добавления: 2016-05-25; просмотров: 1479;
