Дивергенция вектора
Вернемся к рассмотрению течения жидкости и поля вектора скорости  частиц жидкости. Представим в окрестности некоторой точки
частиц жидкости. Представим в окрестности некоторой точки 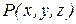 воображаемую замкнутую поверхность
воображаемую замкнутую поверхность 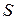 , ограничивающую объем
, ограничивающую объем 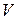 . Если внутри
. Если внутри 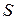 в объеме
в объеме 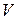 жидкость не исчезает и не появляется, то линии вектора
жидкость не исчезает и не появляется, то линии вектора  (они же линии тока жидкости) непрерывны, и
(они же линии тока жидкости) непрерывны, и 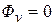 .
.
Если  , то это означает, что внутри
, то это означает, что внутри 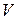 есть источники, мощность которых равна
есть источники, мощность которых равна 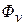 (стоки рассматриваем как источники с отрицательной мощностью). Под мощностью источника подразумевается объем жидкости, выбрасываемый им в единицу времени. Отношение
(стоки рассматриваем как источники с отрицательной мощностью). Под мощностью источника подразумевается объем жидкости, выбрасываемый им в единицу времени. Отношение 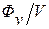 есть средняя удельная мощность источников в
есть средняя удельная мощность источников в 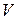 .
.
Поток вектора  через поверхность
через поверхность 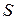 и средняя удельная мощность источников в объеме
и средняя удельная мощность источников в объеме 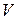 интегрально, по объему
интегрально, по объему 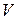 , характеризует характер изменения поля и поведение вектора скорости частиц. Однако очень часто возникает необходимость более детального описания поведения поля вектора скорости, например интенсивности возникновения новых линий вектора в зависимости от координат. С этой целью естественно уменьшить мысленно объем
, характеризует характер изменения поля и поведение вектора скорости частиц. Однако очень часто возникает необходимость более детального описания поведения поля вектора скорости, например интенсивности возникновения новых линий вектора в зависимости от координат. С этой целью естественно уменьшить мысленно объем 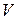 . По определению предел отношения потока вектора
. По определению предел отношения потока вектора  через замкнутую поверхность, ограничивающую некоторый объем в окрестности заданной точки поля, к величине объема
через замкнутую поверхность, ограничивающую некоторый объем в окрестности заданной точки поля, к величине объема 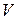 , при его стремлении к нулю, называют дивергенцией соответствующего вектора:
, при его стремлении к нулю, называют дивергенцией соответствующего вектора:
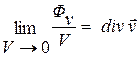 (13.12)
(13.12)
(можно говорить о пределе удельной мощности источников вектора).
Соответственно, по определению, для произвольного вектора 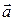 дивергенцией называется величина
дивергенцией называется величина
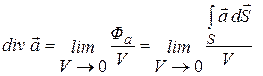 (13.13)
(13.13)
Геометрическая интерпретация потока вектора, как количества пересечений линий вектора с поверхностью, позволяет истолковать дивергенцию вектора 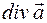 , как функцию, равную плотности точек, в которых начинаются линии
, как функцию, равную плотности точек, в которых начинаются линии 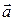 . В точках, где линии вектора заканчиваются дивергенция вектора отрицательна.
. В точках, где линии вектора заканчиваются дивергенция вектора отрицательна.
По смыслу 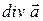 характеризует распределение в пространстве источников силовых линий и определяет плотность мощности источников вектора. Произведение
характеризует распределение в пространстве источников силовых линий и определяет плотность мощности источников вектора. Произведение 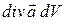 дает мощность источников в объеме
дает мощность источников в объеме 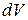 .
.
Такое определение дивергенции не зависит от выбора системы координат, однако, неудобно для вычислений.
13.4 Выражение для 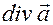 в декартовой системе координат
в декартовой системе координат
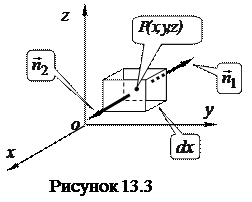 Возьмем в окрестности точки
Возьмем в окрестности точки 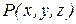 бесконечно малый объем
бесконечно малый объем 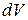 в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат величиной
в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат величиной 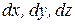 соответственно. Очевидно, что
соответственно. Очевидно, что  .
.
Найдем поток через поверхность, ограничивающую 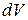 . Для смотрящей на нас грани параллелепипеда единичная внешняя нормаль
. Для смотрящей на нас грани параллелепипеда единичная внешняя нормаль 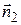 совпадает с направлением оси
совпадает с направлением оси 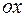 . Поэтому проекция вектора на направление нормали к этой грани
. Поэтому проекция вектора на направление нормали к этой грани
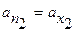 , (13.14)
, (13.14)
где 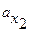 проекция вектора
проекция вектора 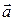 на ось
на ось 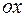 .
.
Для противоположной грани:
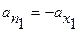 , (13.15)
, (13.15)
Поскольку орт нормали 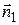 направлен навстречу оси
направлен навстречу оси 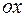 . Тогда суммарный поток вектора
. Тогда суммарный поток вектора 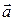 через грани, перпендикулярные оси
через грани, перпендикулярные оси 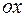 :
:
 . (13.16)
. (13.16)
Изменение проекции 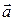 на ось
на ось 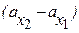 можно найти в виде:
можно найти в виде:
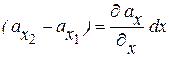 . (13.17)
. (13.17)
Поэтому поток через две грани
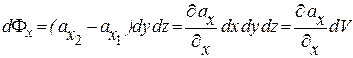 . (13.18)
. (13.18)
Рассуждая аналогичным образом, для граней перпендикулярных двум другим осям системы координат, можно найти значения потоков:
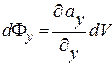 и
и 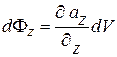 . (13.19)
. (13.19)
Тогда поток через всю поверхность параллелепипеда
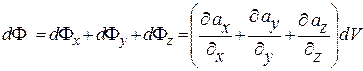 . (13.20)
. (13.20)
Поэтому дивергенцию вектора в декартовой системе координат можно найти, воспользовавшись соотношением:
 . (13.21)
. (13.21)
13.5 Теорема Остроградского – Гаусса.
Знание 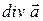 в каждой точке пространства позволяет найти поток вектора через любую поверхность.
в каждой точке пространства позволяет найти поток вектора через любую поверхность.
Поскольку для идеальной жидкости 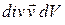 дает мощность источников в бесконечно малом объеме
дает мощность источников в бесконечно малом объеме 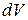 , то в заданном объеме
, то в заданном объеме 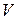 конечных размеров мощность источников определяется соотношением
конечных размеров мощность источников определяется соотношением 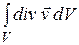 .
.
Вся жидкость, порожденная источниками в объеме 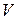 в единицу времени должна, в силу ее несжимаемости, выйти за пределы объема через его поверхность
в единицу времени должна, в силу ее несжимаемости, выйти за пределы объема через его поверхность 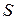 . Но объем жидкости, вытекающий через поверхность
. Но объем жидкости, вытекающий через поверхность 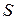 в единицу времени есть поток жидкости через поверхность
в единицу времени есть поток жидкости через поверхность 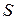 , ограничивающую объем (в соответствии с определением потока вектора скорости частиц жидкости). Поэтому можно утверждать, что справедливо соотношение:
, ограничивающую объем (в соответствии с определением потока вектора скорости частиц жидкости). Поэтому можно утверждать, что справедливо соотношение:
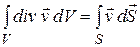 . (13.22)
. (13.22)
Соотношение, аналогичное (13.22)справедливо для любого векторного поля:
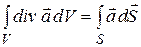 , (13.23)
, (13.23)
и носит название теоремы Остроградского – Гаусса.
Циркуляция
Допустим, что неким фантастическим образом мы можем мгновенно заморозить любой объем некоторой движущейся жидкости. И в некоторый момент времени мы мгновенно замораживаем всю жидкость  , кроме тонкого замкнутого канала постоянного сечения
, кроме тонкого замкнутого канала постоянного сечения 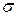 , по центру которого проходит контур
, по центру которого проходит контур  . Возникает вопрос: жидкость в канале остановится, или будет двигаться? Если двигаться, то в каком направлении… Очевидно, что результат зависит от характера течения жидкости, с одной стороны, и ориентации в пространстве канала и контура
. Возникает вопрос: жидкость в канале остановится, или будет двигаться? Если двигаться, то в каком направлении… Очевидно, что результат зависит от характера течения жидкости, с одной стороны, и ориентации в пространстве канала и контура  . Интуитивно понятно, что если говорить о движении жидкости типа течения реки, когда у дна (за счет взаимодействия с ним) скорость частиц должна быть меньше, чем у поверхности, результат будет зависеть от ориентации в пространстве контура. Если плоскость контура совпадает с направлением течения, и и контур расположен вертикально, то в верхней части контура импульс частиц жидкости больше, и это вызовет вращение жидкости в канале. Если представить контур в горизонтальной плоскости, то жидкость вращаться не будет, и т.д.
. Интуитивно понятно, что если говорить о движении жидкости типа течения реки, когда у дна (за счет взаимодействия с ним) скорость частиц должна быть меньше, чем у поверхности, результат будет зависеть от ориентации в пространстве контура. Если плоскость контура совпадает с направлением течения, и и контур расположен вертикально, то в верхней части контура импульс частиц жидкости больше, и это вызовет вращение жидкости в канале. Если представить контур в горизонтальной плоскости, то жидкость вращаться не будет, и т.д.
Для математического описания задачи примем в качестве меры движения жидкости величину произведения скорости движения жидкости на длину, контура 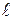 :
: 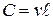 , которую называют циркуляцией.
, которую называют циркуляцией.
В момент затвердевания у частиц жидкости будет погашена составляющая импульса, перпендикулярная стенкам и останется только тангенциальная составляющая. Жидкость в отрезке длиной 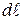 будет иметь импульс
будет иметь импульс 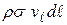 . (
. (  - плотность жидкости,
- плотность жидкости, 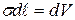 - объем элемента контура длиной
- объем элемента контура длиной 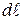 ,
, 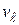 проекция скорости частиц жидкости на направление
проекция скорости частиц жидкости на направление 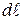 ). Вследствие идеального взаимодействия частиц жидкости происходит выравнивание их импульсов и жидкость начинает двигаться со скоростью
). Вследствие идеального взаимодействия частиц жидкости происходит выравнивание их импульсов и жидкость начинает двигаться со скоростью  . При этом выполняется закон сохранения импульса, так, что импульс жидкости в канале должен быть равен сумме составляющих импульса в элементах канала в направлении контура:
. При этом выполняется закон сохранения импульса, так, что импульс жидкости в канале должен быть равен сумме составляющих импульса в элементах канала в направлении контура:
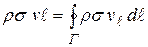 , (13.24)
, (13.24)
Поэтому циркуляция
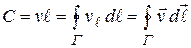 (13.25)
(13.25)
В общем случае циркуляцией вектора 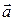 по контуру
по контуру  называют:
называют:
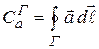 (13.26)
(13.26)
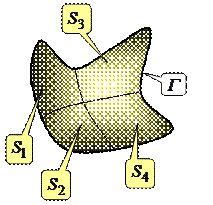 Важнейшим свойством циркуляции является ее аддитивность.То есть если некоторая поверхность
Важнейшим свойством циркуляции является ее аддитивность.То есть если некоторая поверхность 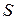 , ограниченная контуром
, ограниченная контуром  разбита на площадки
разбита на площадки  то циркуляция по контуру, ограничивающему
то циркуляция по контуру, ограничивающему 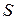 равна сумме циркуляций по контурам, ограничивающим
равна сумме циркуляций по контурам, ограничивающим  :
:
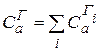 (13.27)
(13.27)
Ротор вектора
Аддитивность циркуляции позволяет ввести понятие об удельной циркуляции, то есть можно рассматривать отношение циркуляции С по контуру ограничивающему S, к величине S: 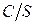 .
.
Для неаддитивной величины рассматривать ее удельную величину бессмысленно. Например, возьмем удельную температуру площадки S:  . Температура величина неаддитивная, и от деления площадки на части не меняется. Если площадку разделить на части
. Температура величина неаддитивная, и от деления площадки на части не меняется. Если площадку разделить на части 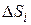 , то их «удельная Т» будет возрастать, при уменьшении
, то их «удельная Т» будет возрастать, при уменьшении 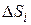 , до бесконечности, ничего не характеризуя. Если взять аддитивную величину массу, то удельная масса площадки в «
, до бесконечности, ничего не характеризуя. Если взять аддитивную величину массу, то удельная масса площадки в « 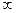 » не уходит, а является поверхностной плотностью площадки, характеризует распределение массы по поверхности. Циркуляция величина аддитивная, и об удельной циркуляции имеет смысл говорить.
» не уходит, а является поверхностной плотностью площадки, характеризует распределение массы по поверхности. Циркуляция величина аддитивная, и об удельной циркуляции имеет смысл говорить.
Однако, удельная циркуляция является макроскопической характеристикой, усреднённо характеризует свойства поля в пределах площадки S. Для описания свойств поля в точке можно использовать удельнную циркуляцию в точке  :
:
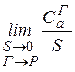 . (13.28)
. (13.28)
Этот предел зависит не только от способности данного поля «создавать» циркуляцию, но и от ориентации в пространстве площадки S, то есть контура ее ограничивающего. Ориентацию контура принято задавать направлением положительной нормали, направление которой связано с направлением обхода контура при вычислении циркуляции, правилом правого винта.
Предел (13.28),найденныйдля противоположно ориентированных положительных 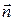 , отличается только знаком. Противоположным направлениям
, отличается только знаком. Противоположным направлениям 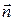 соответствует противоположные
соответствует противоположные 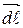 при вычислении
при вычислении 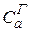 . Существуют такие направления,
. Существуют такие направления, 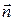 , для которых предел (13.28) достигает максимального значения и такие, когда обращается в нуль.
, для которых предел (13.28) достигает максимального значения и такие, когда обращается в нуль.
Получается, что предел (13.28)ведет себя как проекция некоторого вектора на ось, направленную в сторону нормали, соответствующей максимальному значению предела 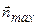 .Если этот вектор направлен в сторону
.Если этот вектор направлен в сторону 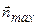 , его проекция максимальна, если он ей перпендикулярен, проекция равна нулю, и проекция отрицательна для направления, противоположного
, его проекция максимальна, если он ей перпендикулярен, проекция равна нулю, и проекция отрицательна для направления, противоположного 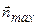 .
.
Этот вектор и называется ротором вектора 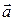 и обозначается
и обозначается
 .
.
Максимальное значение предела (13.28)определяет модуль 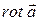 , а соответствующее направление нормали
, а соответствующее направление нормали 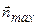 – направление
– направление 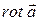 .
.
Таким образом, можно утверждать, что при произвольной ориентации контура предел (13.28) дает проекцию ротора на направление нормали 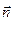 , задающей ориентацию контура в пространстве:
, задающей ориентацию контура в пространстве:
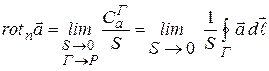 . (13.29)
. (13.29)
13.8 Выражение для 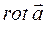 в декартовой системе координат
в декартовой системе координат
 Соотношение (13.29) позволяет найти проекцию ротора вектора на заданное направление. Поскольку
Соотношение (13.29) позволяет найти проекцию ротора вектора на заданное направление. Поскольку 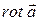 является вектором, для его определения необходимо задать его проекции на оси координат. Это позволит найти вектор в целом:
является вектором, для его определения необходимо задать его проекции на оси координат. Это позволит найти вектор в целом:
 (13.30)
(13.30)
Поэтому представим контур в виде прямоугольника со сторонами, параллельными осям координат 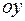 и
и 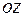 (рисунок 13.5). Выберем направление обхода контура так, как указано стрелками, чтобы нормаль к контуру совпадала с направлением оси
(рисунок 13.5). Выберем направление обхода контура так, как указано стрелками, чтобы нормаль к контуру совпадала с направлением оси 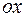 . Площадь контура равна
. Площадь контура равна 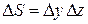 . Найдем циркуляцию по такому контуру и, разделив ее на площадь контура, получим выражение для проекции ротора на ось
. Найдем циркуляцию по такому контуру и, разделив ее на площадь контура, получим выражение для проекции ротора на ось 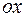 .
.
На участке 1 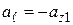 , поскольку на этом участке элементы контура направлены навстречу оси
, поскольку на этом участке элементы контура направлены навстречу оси 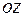 . На участке 3
. На участке 3  . Аналогичные соотношения справедливы и для участков 2 и 4. Будем считать
. Аналогичные соотношения справедливы и для участков 2 и 4. Будем считать 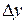 и
и  достаточно малыми, чтобы проекцию вектора
достаточно малыми, чтобы проекцию вектора 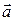 на этих участках можно было бы считать постоянной. Тогда для циркуляции по контуру можно записать:
на этих участках можно было бы считать постоянной. Тогда для циркуляции по контуру можно записать:
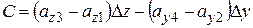 . (13.31)
. (13.31)
Приращение составляющей 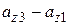 при смещении на
при смещении на 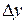 представим в виде:
представим в виде:
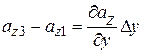 . (13.32)
. (13.32)
Соответственно
 . (13.33)
. (13.33)
Поэтому циркуляция по контуру, ориентированному нормалью вдоль 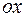 :
:
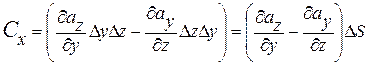 . (13.34)
. (13.34)
Разделим на 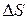 , и для проекции ротора на ось
, и для проекции ротора на ось 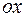 получим:
получим:
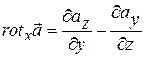 . (13.35)
. (13.35)
Рассуждая аналогичным образом для проекций на 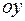 и
и 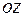 можем записать:
можем записать:
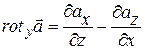 , (13.36)
, (13.36)
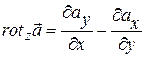 . (13.37)
. (13.37)
Осталось подставить найденные проекции ротора в формулу (13.30):
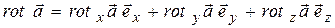 .
.
Теорема Стокса
Знание  в каждой точке поверхности S позволяет найти циркуляцию по контуру Г, ограничивающему S. Для этого разобьем S на малые
в каждой точке поверхности S позволяет найти циркуляцию по контуру Г, ограничивающему S. Для этого разобьем S на малые 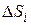 , каждую из которых можно считать плоской и описывать вектором
, каждую из которых можно считать плоской и описывать вектором  . Тогда
. Тогда
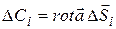 . (13.38)
. (13.38)
В силу аддитивности циркуляции, циркуляция по контуру Г, ограничивающему S
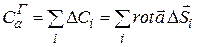 . (13.39)
. (13.39)
В пределе, при  , учитывая, что
, учитывая, что 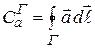 , получаем :
, получаем :
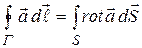 . (13.40)
. (13.40)
Это соотношение называют теоремой СТОКСА.
13.10 Представление градиента, дивергенции и ротора с использованием оператора Ñ
Запись формул векторного анализа существенно упрощается при использовании векторного дифференциального оператора Ñ:
 . (13.41)
. (13.41)
Если Ñ умножить на скалярную функцию 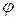 :
:
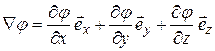 , то получаем
, то получаем 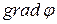 . Поэтому часто вместо
. Поэтому часто вместо
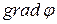 пишут
пишут 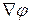 . Итак:
. Итак:
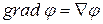 . (13.42)
. (13.42)
Если Ñ скалярно умножить на векторную функцию 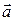 , то получится скаляр
, то получится скаляр
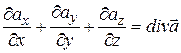 . (13.43)
. (13.43)
Если же Ñ умножить на вектор 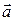 векторно, то получим
векторно, то получим
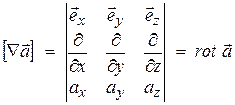 . (13.44)
. (13.44)
Дата добавления: 2016-06-02; просмотров: 4728;
