Выполнение действий с векторами через их координаты
В координатной форме записи удобно выполнять любые действия с векторами.
Чтобы умножить вектор на число, нужно все его координаты умножить на это число:
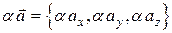 .
.
Чтобы найти сумму или разность векторов, нужно сложить или вычесть соответствующие координаты.
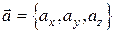 ;
; 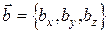 ;
;
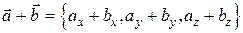 ;
; 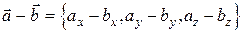 .
.
Используя свойства скалярного произведения, а также тот факт, что базисные вектора взаимно ортогональны, можно получить формулу для вычисления скалярного произведения векторов, заданных своими координатами:
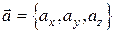 ;
; 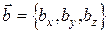 ;
;
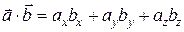 .
.
Скалярное произведение векторов равно сумме произведений соответствующих координат.
Такое определение пригодно и для случая векторов с произвольным числом координат - n-мерных векторов.
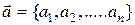 ;
; 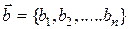 ;
;
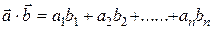 .
.
Формула для вычисления угла между векторами:
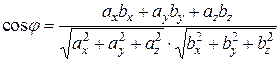
Учитывая свойства векторного произведения и взаимную перпендикулярность базисных векторов, можно получить способ определения координат векторного произведения через координаты входящих в него векторов 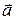 и
и 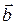 .
.
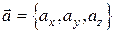 ;
; 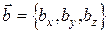 ;
;
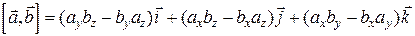 .
.
Формулы для вычисления координат векторного произведения легче запоминаются, если представить его в виде определителя, составленного из базисных векторов и координат векторов 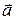 и
и 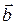 , разложенного по элементам первой строки:
, разложенного по элементам первой строки:
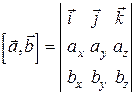
Смешанное произведение легко вычисляется, если вектора 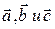 заданы своими координатами:
заданы своими координатами:
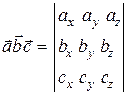
Смешанное произведение равно определителю, составленному из координат векторов, входящих в смешанное произведение.
Пример 1. В пирамиде с вершинами в точках 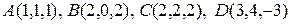 найти длину высоты, опущенной из вершины
найти длину высоты, опущенной из вершины 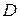 .
.
Для нахождения высоты используем формулу, связывающую объем пирамиды 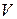 , площадь основания
, площадь основания 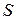 и высоту пирамиды
и высоту пирамиды  :
:
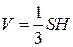 .
.
Из указанной формулы найдем 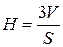 .
.
Данную пирамиду можно считать построенной на векторах 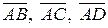 . Заметим, что векторы, на которых построена пирамида, должны выходить их общей вершины. Объем пирамиды найдем как 1/6 модуля смешанного произведения указанных векторов:
. Заметим, что векторы, на которых построена пирамида, должны выходить их общей вершины. Объем пирамиды найдем как 1/6 модуля смешанного произведения указанных векторов:
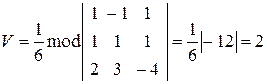 .
.
Координаты самих векторов найдены так, как описано в п. 18.1. Основанием является треугольник 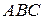 , его площадь найдем как половину модуля векторного произведения векторов, на которых он построен
, его площадь найдем как половину модуля векторного произведения векторов, на которых он построен 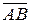 и
и 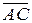 . Вначале найдем само векторное произведение:
. Вначале найдем само векторное произведение:
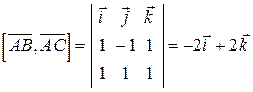 .
.
Тогда 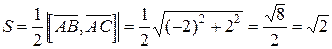 .
.
Теперь найдем высоту 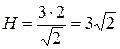 .
.
Пример 2. Найти внутренние углы треугольника с вершинами 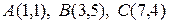 .
.
Угол 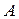 образован векторами
образован векторами 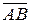 и
и 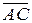 , угол
, угол 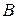 – векторами
– векторами 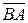 и
и 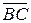 , угол
, угол 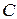 – векторами
– векторами 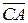 и
и 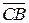 , выпишем координаты всех нужных векторов:
, выпишем координаты всех нужных векторов:
 .
.
Найдем косинусы всех углов треугольника:
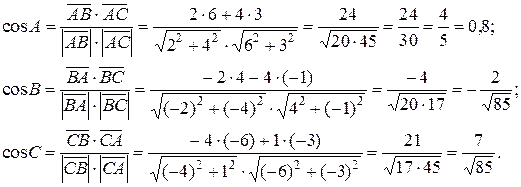
Найдем углы:
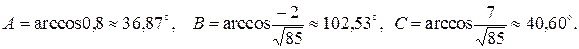
Сделаем проверку: 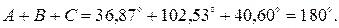
Дата добавления: 2016-10-17; просмотров: 1131;
