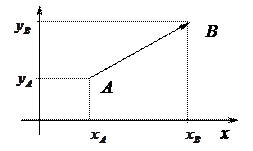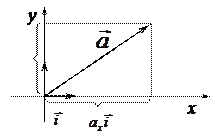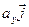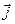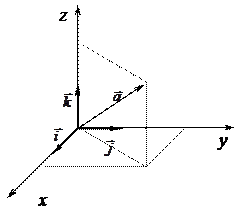Представление векторов в координатной форме
|
|
|
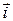 и
и 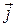 . Тогда любой вектор
. Тогда любой вектор 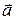 можно представить в виде суммы некоторого числа
можно представить в виде суммы некоторого числа 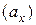 векторов
векторов 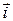 и некоторого числа
и некоторого числа 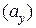 векторов
векторов 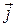 :
: 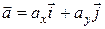 .
.
Кратко такая сумма записывается так: 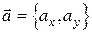 . Числа
. Числа 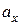 и
и 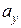 равны проекциям вектора
равны проекциям вектора 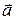 на соответствующие оси и называются координатами вектора.
на соответствующие оси и называются координатами вектора.
Следует отметить, что одни и те же координаты могут иметь векторы, приложенные к разным точкам. Чтобы устранить эту неопределенность, можно указывать координаты начала 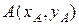 и конца
и конца 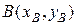 вектора. Нетрудно видеть, что координаты вектора
вектора. Нетрудно видеть, что координаты вектора 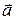 можно найти через координаты начала и конца по следующему правилу:
можно найти через координаты начала и конца по следующему правилу:
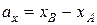 ;
; 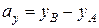 .
.
Вспомнив теорему Пифагора, можно найти и длину вектора:
 .
.
|
Чтобы представить вектор в пространстве (трехмерный вектор) по трем взаимно перпендикулярным осям (OX, OY и OZ) откладываются базисные вектора единичной длины 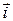 ,
, 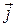 ,
, 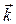 . Тогда любой вектор
. Тогда любой вектор 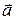 можно представить в виде суммы некоторого числа
можно представить в виде суммы некоторого числа 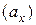 векторов
векторов 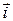 , некоторого числа
, некоторого числа 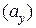 векторов
векторов 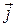 и некоторого числа
и некоторого числа 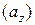 векторов
векторов 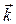 :
:
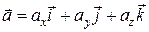 .
.
Краткая запись: 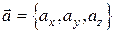 . Числа
. Числа 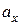 ,
, 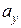 ,
, 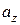 равны проекциям
равны проекциям 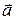 на координатные оси OX, OY u OZ и называются координатами вектора
на координатные оси OX, OY u OZ и называются координатами вектора 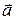 . Чтобы уточнить положение вектора, можно так же, как и на плоскости указать координаты начала А и конца В вектора
. Чтобы уточнить положение вектора, можно так же, как и на плоскости указать координаты начала А и конца В вектора 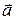 :
: 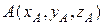 и
и 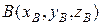 . Связь между координатами вектора и координатами начала и конца:
. Связь между координатами вектора и координатами начала и конца:
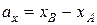 ;
; 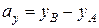 ;
; 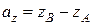 .
.
Длина трехмерного вектора вычисляется по формулам:
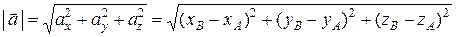 .
.
Если условиться помещать начало вектора в начало координат, то вектор на плоскости (двумерный) можно записывать двойкой чисел, вектор в пространстве (трехмерный) - тройкой. Рассуждая подобным образом и дальше, можно предположить, что четыре числа соответствуют четырехмерному вектору, пять - пятимерному и т.д. n чисел - n-мерному вектору. И вообще, любая величина, записываемая упорядоченным набором чисел, часто называется вектором.
Дата добавления: 2016-10-17; просмотров: 5277;