Лекция № 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТИРКАХ
15.1 ПОЛЯРНЫЕ И НЕПОЛЯРНЫЕ МОЛЕКУЛЫ.
Веществ, абсолютно не проводящих электрический ток в природе не существует. Поэтому диэлектриками или изоляторами называют вещества, которые проводят электрический ток в 1015 ¸ 1020 раз хуже, чем металлы. При внесении диэлектрика в электрическое поле в нем происходят существенные изменения, для понимания которых необходимо помнить о том, что в состав атомов и молекул любого диэлектрика входят тяжелые положительно заряженные ядра и намного более легкие отрицательно заряженные электроны. Поэтому с точки зрения электрических свойств нейтральная молекула представляет собой систему положительных и отрицательных зарядов с очень малыми размерами. Электрическое поле, создаваемое такой системой определяется ее дипольным электрическим моментом:
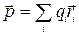 (15.1)
(15.1)
Дипольный электрический момент определяет также и поведение молекулы во внешнем электрическом поле. Необходимо, однако, учитывать, что электроны в молекулах движутся и с весьма большими скоростями. Так что дипольный электрический момент 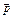 молекулы быстро изменяется с течением времени. Практически можно наблюдать только среднее значение дипольного электрического момента:
молекулы быстро изменяется с течением времени. Практически можно наблюдать только среднее значение дипольного электрического момента:
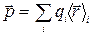 , (15.2)
, (15.2)
о котором мы и будем говорить в дальнейшем.
Аналогично центру тяжести механической системы можно ввести в рассмотрение центры тяжести положительных и отрицательных зарядов молекулы, положение которых определяется радиус-векторами:
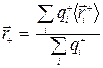 ;
; 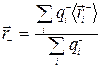 (15.3)
(15.3)
Тогда молекулу можно рассматривать как диполь, положительный заряд которого расположен в центре тяжести положительных зарядов, а отрицательный соответственно в центре тяжести отрицательных зарядов.
У симметричных молекул (например, H2 ,O2, N2) в отсутствие электрического поля центры тяжести положительных и отрицательных зарядов совпадают. Такие молекулы не имеют собственного дипольного электрического момента и называются неполярными. У несимметричных молекул (например, H2O, Н Cl) центры тяжести положительных и отрицательных зарядов не совпадают, они обладают собственным дипольным электрическим моментом и называются полярными.
Во внешнем электрическом поле полярные и неполярные молекулы ведут себя по-разному. В неполярной молекуле заряды смещаются друг относительно друга, и молекула приобретает дипольный электрический момент, направленный по полю и пропорциональный напряженности внешнего поля:
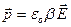 (15.3)
(15.3)
где коэффициент пропорциональности  называют поляризуемостью молекулы. Другими словами заряды в неполярной молекуле ведут себя так, как будто они связаны упругой связью. Поэтому неполярные молекулы во внешнем электрическом поле ведут себя как упругий диполь.
называют поляризуемостью молекулы. Другими словами заряды в неполярной молекуле ведут себя так, как будто они связаны упругой связью. Поэтому неполярные молекулы во внешнем электрическом поле ведут себя как упругий диполь.
На полярные молекулы внешнее поле оказывает в основном ориентирующее действие. Поэтому говорят, что полярная молекула ведет себя во внешнем электрическом поле как жесткий диполь.
15.2 ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
Обычно, в отсутствие электрического поля, суммарный дипольный момент диэлектрика равен нулю. Для диэлектриков с неполярными молекулами этот факт очевиден, а у диэлектриков с полярными молекулами хаотическое тепловое движение приводит к хаотическому распределению в пространстве направлений дипольных моментов так, что результирующий момент тоже оказывается нулевым.
Во внешнем электрическом поле результирующий дипольный момент диэлектрика становится отличным от нуля, говорят, что диэлектрик поляризуется. В качестве величины, характеризующей степень поляризации диэлектрика естественно использовать дипольный момент единицы объема диэлектрика. Однако такая величина будет характеризовать поляризацию усредненно. Поэтому для характеристики поляризации используется векторная величина называемая поляризованностьюдиэлектрика, которая по определению равна отношению результирующего дипольного момента физически бесконечно малого объема к величине этого объема:
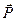
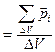 (15.5)
(15.5)
Если однородный диэлектрик помещен в однородное электрическое поле, то 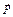 совпадает с электрическим моментом единицы объема диэлектрика. Экспериментально установлено, что у изотропных диэлектриков поляризованность пропорциональна напряженности поля в данной точке:
совпадает с электрическим моментом единицы объема диэлектрика. Экспериментально установлено, что у изотропных диэлектриков поляризованность пропорциональна напряженности поля в данной точке:
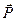
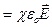 (15.6)
(15.6)
где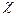 - независящая от
- независящая от 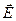 величина, называемая диэлектрической восприимчивостью диэлектрика.
величина, называемая диэлектрической восприимчивостью диэлектрика.
У неполярных диэлектриков соотношение (15.6) вытекает из формулы (15. 4). Действительно, если концентрация молекул равна n , то в объем 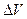 попадают
попадают 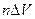 молекул с дипольными моментами
молекул с дипольными моментами 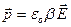 . Следовательно
. Следовательно
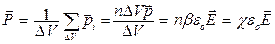 (15.7)
(15.7)
У диэлектриков с полярными молекулами ориентирующему действию электрического поля противодействует тепловое движение, поэтому в данном поле устанавливается некоторая преимущественная ориентация дипольных моментов. При этом соотношение (15.6) остается справедливым.
У ионных кристаллов отдельные молекулы утрачивают обособленность. Весь кристалл можно рассматривать как гигантскую молекулу. Решетка такого кристалла представляет две вставленные друг в друга подрешетки, из которых одна образована положительными ионами, а другая - отрицательными, В электрическом поле подрешетки смешиваются друг относительно друга , т.е. кристалл поляризуется. Соотношение (15.6) справедливо и в этом случае.
15.3. ПОЛЕ ВНУТРИ ДИЭЛЕКТРИКА
Заряды, входящие в состав молекул диэлектрика будем называть связанными. Под действием поляэти заряды могут смещаться из своих положений равновесия, однако покинуть пределы молекулы они не могут. Заряды, расположенные вне диэлектрика, а также заряды внутри объема диэлектрика, но не входящие в состав молекул, будем называть сторонними. (Их называют также свободными.)
Результирующее микроскопическое поле в диэлектрике 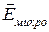 является суперпозицией поля сторонних зарядов
является суперпозицией поля сторонних зарядов 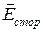 и поля связанных зарядов
и поля связанных зарядов 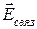 .
.
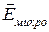 =
= 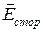 +
+ 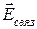 (15.8)
(15.8)
Это поле называют истинным или микроскопическим. Однако это поле неудобно использовать при описании свойств диэлектриков, т.к. оно сильно изменяется в пределах межатомных расстояний, а также со временем, вследствие движения молекул. При описании макроскопических свойств эти изменения не обнаруживаются, и в качестве характеристики поля используется усредненное значение 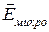 :
:
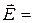
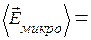
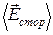 +
+  (15.9)
(15.9)
Обычно усредненное поле сторонних зарядов обозначают  , а усредненное поле связанных зарядов -
, а усредненное поле связанных зарядов -  , и записывают:
, и записывают:

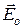 +
+ 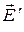 (15.10)
(15.10)
Именно поле, определяемое формулой (15.10), подразумевается в соотношении (15.6), и его называют макроскопическим полем.
15.4 ЯВЛЕНИЯ НА ПОВЕРХНОСТИ ДИЭЛЕКТРИКА.
В неполяризованном диэлектрике объемная 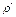 и поверхностная
и поверхностная  плотности связанных зарядов равны нулю. В результате поляризации поверхностная, а в ряде случаев и объемная, плотности зарядов становятся отличными от нуля. Рассмотрим процессы, происходящие при этом.
плотности связанных зарядов равны нулю. В результате поляризации поверхностная, а в ряде случаев и объемная, плотности зарядов становятся отличными от нуля. Рассмотрим процессы, происходящие при этом.
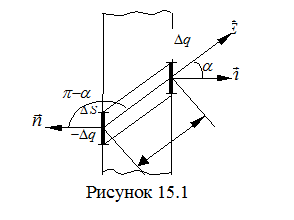 Вполне очевидно, что если для данного участка поверхности диэлектрика нормальная составляющая электрического доля отлична от нуля, то в тонком приповерхностном слое возникает связанный заряд одного знака, т. к. под действием поля заряды одного знака уходят внутрь диэлектрика, а другого - выходят наружу. Естественно предположить, что между степенью поляризации, т.е. поляризованностью
Вполне очевидно, что если для данного участка поверхности диэлектрика нормальная составляющая электрического доля отлична от нуля, то в тонком приповерхностном слое возникает связанный заряд одного знака, т. к. под действием поля заряды одного знака уходят внутрь диэлектрика, а другого - выходят наружу. Естественно предположить, что между степенью поляризации, т.е. поляризованностью 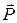 ,и
,и 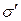 должна существовать связь. Для ее нахождения рассмотрим бесконечную плоскопараллельную пластинку однородного диэлектрика, помещенную в однородное электрическое поле. Мысленно выделим в пластинке элементарный объем
должна существовать связь. Для ее нахождения рассмотрим бесконечную плоскопараллельную пластинку однородного диэлектрика, помещенную в однородное электрическое поле. Мысленно выделим в пластинке элементарный объем 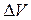 в виде тонкого цилиндра с основаниями площади
в виде тонкого цилиндра с основаниями площади 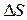 и образующими, параллельными
и образующими, параллельными 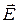 . Если расстояние между основаниями равно
. Если расстояние между основаниями равно 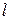 , а угол между
, а угол между 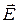 и нормалью к поверхности пластинки
и нормалью к поверхности пластинки 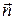 равен
равен 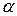 , то
, то
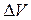 =
= 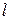
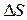 cos
cos 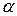 (15.11)
(15.11)
Объем 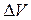 имеет дипольный электрический момент
имеет дипольный электрический момент
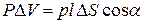 15.12)
15.12)
где Р - модуль вектора поляризованности.
С другой стороны рассматриваемый объем эквивалентен диполю, об разованному зарядами 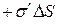 и
и 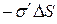 , отстоящими друг от друга на расстояние
, отстоящими друг от друга на расстояние 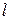 . С этой точки зрения его дипольный момент равен
. С этой точки зрения его дипольный момент равен
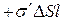 (15.13)
(15.13)
Приравнивая (15.12) и (15.13), получаем:
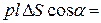
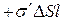 (15.14)
(15.14)
Из (15.14) вытекает соотношение между Р и 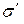 :
:
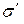
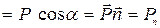 (15.15)
(15.15)
Выразив Р через напряженность электрического поля, придем к соотношению:
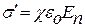 (15.16)
(15.16)
Из (16) вытекает, что в тех местах поверхности, где линии напряженности выходят из диэлектрика, т.е. 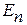 > 0 , на поверхности выступают положительные связанные заряды, а в тех, где входят, т.е.
> 0 , на поверхности выступают положительные связанные заряды, а в тех, где входят, т.е. 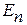 < 0, на поверхности появляются отрицательные связанные заряды.
< 0, на поверхности появляются отрицательные связанные заряды.
В заключение отметим, что формулы (15.15) и (15.16) справедливы и в общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле. В этом случае под 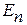 и
и 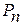 надо понимать нормальные составляющие, взятые в непосредственной близости к тому элементу поверхности, для которого определяется
надо понимать нормальные составляющие, взятые в непосредственной близости к тому элементу поверхности, для которого определяется 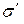 .
.
15.5. ЯВЛЕНИЯ В ОБЪЕМЕ ДИЭЛЕКТРИКА
Рассмотрим теперь условия возникновения в объеме диэлектрика объемной плотности связанных зарядов. Для этого представим внутри неоднородного изотропного диэлектрика с неполярными молекулами воображаемую малую площадку 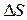 . Пусть в единице объема диэлектрика имеется N одинаковых частиц с зарядом
. Пусть в единице объема диэлектрика имеется N одинаковых частиц с зарядом  и столько же связанных с ними одинаковых отрицательно заряженных частиц с зарядом
и столько же связанных с ними одинаковых отрицательно заряженных частиц с зарядом 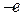 . Поскольку рассматриваемая площадка
. Поскольку рассматриваемая площадка 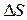 мала, то в ее окрестности поле можно считать однородным, и сам диэлектрик - тоже однородным. При включении электрического поля
мала, то в ее окрестности поле можно считать однородным, и сам диэлектрик - тоже однородным. При включении электрического поля 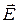 все положительно заряженные частицы сместятся в направлении поля на расстояние
все положительно заряженные частицы сместятся в направлении поля на расстояние 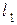 , а все отрицательные - в противоположном направлении на
, а все отрицательные - в противоположном направлении на  . При этом через площадку
. При этом через площадку 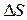 в направлении нормали к ней перейдут положительно заряженные частицы, которые до включения поля находились в объеме косого цилиндра с объемом
в направлении нормали к ней перейдут положительно заряженные частицы, которые до включения поля находились в объеме косого цилиндра с объемом
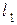
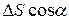 (15.17)
(15.17)
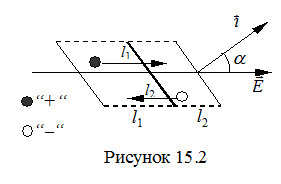 Число таких частиц будет равно
Число таких частиц будет равно 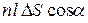 , и они перенесут через
, и они перенесут через 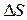 заряд
заряд
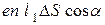 (15.18)
(15.18)
Одновременно отрицательные частицы перенесут через 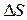 отрицательный заряд в направлении, противоположном
отрицательный заряд в направлении, противоположном 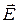 , величиной
, величиной
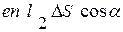 (15.19)
(15.19)
Перенос отрицательного заряда в этом направлении эквивалентен переносу положительного заряда в противоположном направлении. Таким образом, в направлении нормали переносится положительный заряд:
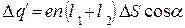 (15.20)
(15.20)
Учтем теперь, что 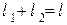 - расстоянию, на которое смещаются при включении поля положительные и отрицательные заряды друг относительно друга. При этом каждая пара зарядов создает дипольный момент р =el . Число таких пар в единице объема равно n. Следовательно,
- расстоянию, на которое смещаются при включении поля положительные и отрицательные заряды друг относительно друга. При этом каждая пара зарядов создает дипольный момент р =el . Число таких пар в единице объема равно n. Следовательно, 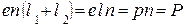 - модулю вектора поляризованности. Таким образом, заряд, проходящий через
- модулю вектора поляризованности. Таким образом, заряд, проходящий через 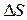 в направлении нормали к ней при включении поля равен
в направлении нормали к ней при включении поля равен
 (15.21)
(15.21)
Мы рассматриваем изотропный диэлектрик, а в нем направления векторов 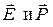 совпадают. Следовательно,
совпадают. Следовательно, 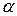 есть угол между
есть угол между 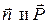 . Тогда можно записать, что
. Тогда можно записать, что
 (15.22)
(15.22)
Переходя к дифференциалам, получаем, что черезэлементарную площадку  в направлении нормали к ней проходит заряд
в направлении нормали к ней проходит заряд
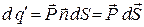 (15.23)
(15.23)
Представим теперь себе внутри объема диэлектрика замкнутую поверхность S. Напомним, что в случае замкнутых поверхностей положительной считается внешняя нормаль. Тогда при включении поля через S выйдет наружу связанней заряд:
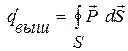 (15.24)
(15.24)
Следовательно, в объеме, ограниченном S, возникнет избыточный связанный заряд:
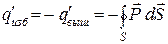 (15.25)
(15.25)
Если объемная плотность этого связанного заряда равна 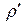 , то
, то
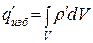 (15.26)
(15.26)
Приравнивая правые части (15.25) и (15.26), получаем:
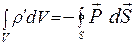 (15.27)
(15.27)
Поверхностный интеграл в (15.27) преобразуем по теореме Остроградского-Гаусса:
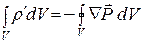 (15.28)
(15.28)
Соотношение (15.28) должно выполняться для произвольного объема V , а это возможно только в том случае, если в каждой точке диэлектрика
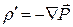 (15.29)
(15.29)
Таким образом, плотность связанных зарядов в диэлектрике равна дивергенции вектора поляризованности, взятой с обратным знаком. Это утверждение справедливо и для диэлектриков с полярными молекулами.
Выясним более конкретно, при каких условиях в диэлектрике возможно возникновение объемного связанного заряда. Воспользуемся связью поляризованности и напряженности электрического поля 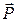
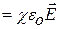 (15.6), подставим в (15.29) и осуществим дифференцирование:
(15.6), подставим в (15.29) и осуществим дифференцирование:
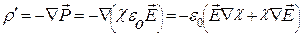 (15.30)
(15.30)
Учтем, что связанные заряды ничем кроме своей связанности не отличаются от сторонних, и также являются источниками электрического поля. Поэтому выражение теоремы Гаусса в рассматриваемом случае следует записать в виде:
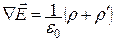 (15.31)
(15.31)
Подставим выражение для 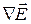 из (15.31) в (15.30):
из (15.31) в (15.30):
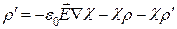 (15.32)
(15.32)
Выразим  из (15.32):
из (15.32):
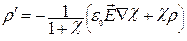 (15.33)
(15.33)
На основании (15.33) можно утверждать, что объемная плотность связанных зарядов в диэлектрике может быть отлична от нуля в двух случаях:
1) если диэлектрик неоднороден, т.е. Ñc¹ 0 (например, в области границы раздела двух сред);
2) если в данном месте диэлектрика отлична от нуля плотность сторонних зарядов, т.е. внутрь диэлектрика каким-либо образом введен сторонний заряд.
15.6 Вектор электрического смещения
Как мы уже отмечали, источниками электрического поля в диэлектрике являются и сторонние и связанные заряды, поэтому по теореме Гаусса:
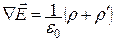 (15.34)
(15.34)
Однако формула (15.34) фактически не позволяет находить напряженность электрического поля 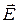 , т. к. плотность связанных зарядов в свою очередь выражается через
, т. к. плотность связанных зарядов в свою очередь выражается через 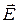 , как это следует из формул (15.16), (15.32):
, как это следует из формул (15.16), (15.32):
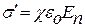 ;
; 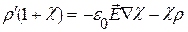
Для упрощения вычисления электрических полей можно ввести в рассмотрение вспомогательную величину, источникам которой будут только сторонние заряды. Для получения соотношения, определяющего эту величину, подставим в (15.34) выражение для  через вектор поляризованности:
через вектор поляризованности: 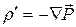 :
:
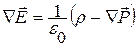 (15.35)
(15.35)
Из (15.35) следует,
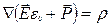 (15.36)
(15.36)
т.е. дивергенция величины, стоящей в скобках, определяется только плотностью сторонних зарядов. По определению векторную величину
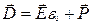 (15.37)
(15.37)
называют электрическим смешением или электрической индукцией. Подставив в (15.37) выражение для поляризации (15.7) 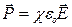 , получим:
, получим:
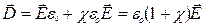 (15.38)
(15.38)
Безразмерную величину
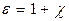 (15.39)
(15.39)
называют относительной диэлектрической проницаемостью. Теперь (15.38) можно представить в виде:
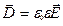 . (15.38)
. (15.38)
Таким образом, между векторами 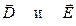 существует очень простая связь, но дивергенция
существует очень простая связь, но дивергенция 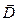 определяется только сторонними зарядами (15.36), поэтому находить электрическую индукцию во многих случаях оказывается проще, а диэлектрическая проницаемость достаточно просто определяется экспериментально.
определяется только сторонними зарядами (15.36), поэтому находить электрическую индукцию во многих случаях оказывается проще, а диэлектрическая проницаемость достаточно просто определяется экспериментально.
В соответствии с (15.36)
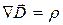 (15.40)
(15.40)
Это выражение можно рассматривать как теорему Гаусса для вектора 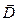 в дифференциальной форме. Возьмем (15.40) интеграл по произвольному объему и применим теорему Остроградского – Гаусса:
в дифференциальной форме. Возьмем (15.40) интеграл по произвольному объему и применим теорему Остроградского – Гаусса:
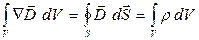 , (15.41)
, (15.41)
т.е. поток вектора электрической индукции через замкнутую поверхность равен алгебраической сумме заключенных внутри нее сторонних зарядов – теорема Гаусса для 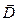 в интегральной форме.
в интегральной форме.
Дата добавления: 2016-06-02; просмотров: 1333;
