Циркуляция и дивергенция электростатического поля
Циркуляция и ротор электростатического поля
Силы электростатического поля являются консервативными. Поэтому их работа на любом замкнутом пути равна нулю:
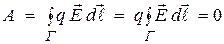. (14.55)
Следовательно, циркуляция вектора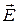 
по любому контуру
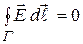. (14.56)
Согласно теореме Стокса,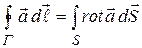 
. Поэтому поток 
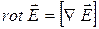через любую поверхность S, опирающуюся на некоторый Г
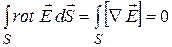(14.57)
Поскольку (14.57) выполняется для любой поверхности, то должно быть равно нулю подынтегральное выражение:
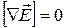(14.58)
Формулы(14.56) и(14.58)означают: невозможно существование электростатического поля такой конфигурации, где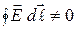 
. Например, невозможно создать электростатическое поле, отличное от нуля только в определенном объёме. Действительно, по всякому контуру, частично проходящему в этом объеме, циркуляция будет не равна нулю, чего быть не может!
Равенство нулю 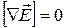указывает на то, что 
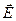можно представить в виде градиента скалярной функции. некоторой скалярной 
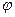. И действительно
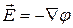(14.59)
Теорема Гаусса
Вспомним о том, что поток любого вектора через замкнутую поверхность численно равен количеству линий, выходящих из поверхности наружу. Мы доказывали, что количество линий выходящих из положительного заряда одинаково на любом расстоянии от него и равно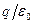 
. Поэтому для точечного заряда справедливо соотношение:
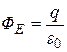(14.60)
Если внутри некоторой замкнутой поверхности S находится N зарядов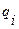 
, то по принципу суперпозиций 
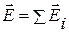. Поэтому поток результирующего поля через поверхность S:
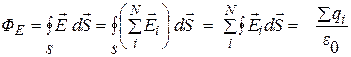(14.61)
Таким образом, можно утверждать, что поток вектора напряженности электростатического поля, через замкнутую поверхность
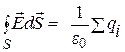, (14.62)
т.е. равен алгебраической сумме зарядов внутри этой поверхности деленной на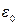 
. Это утверждение называется теоремой Гаусса для вектора напряженности электростатического поля.
Учитывая малость элементарного заряда обычно при рассмотрении макроскопических задач распределение заряда в пространстве, описывают плотностью заряда:
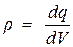, (14.63)
Соответственно соотношение (14.60)записывают в виде
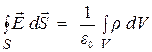, (14.64)
Необходимо учесть, что по теореме Остроградского - Гаусса
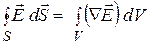. Поэтому
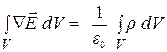, (14.65)
Это равенство должно выполняться для любого объема V, а значит
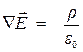, (14.66)
Соотношение (13.66) называется теоремой Гаусса в дифференциальной форме.
Дата добавления: 2016-06-02; просмотров: 1708;