Напряженность электростатического поля.

Закон Кулона показывает, что сила электрического взаимодействия проявляется только между двумя заряженными телами.

Если в формуле:

,

являющейся математической формой закона Кулона, положить q₂ = 0, то и F = 0 при любом значении q₁. Мы знаем, однако, что заряженное тело способно притягивать ненаэлектризованные тела, например, кусочки бумаги или металлической фольги. Все тела (кусочки бумаги) вблизи заряженного тела испытывают электризацию, в результате которой имеющиеся в этих телах заряды перераспределяются так, что в одной части тела накапливаются заряды одного знака, а в другой – другого. При этом, ближе к влияющему заряженному телу оказываются заряды, знак которых противоположен знаку его заряда; одноименные же заряды скапливаются в избытке на отдаленном конце.

Взаимодействие заряда тела с наведенными зарядами происходит по закону Кулона. Поэтому каждое тело с наведенными зарядами одновременно и притягивается и отталкивается заряженным телом. Но отталкивание, имеющее место между зарядами, находящимися на большем расстоянии, слабее, чем притяжение. В результате, «незаряженные» тела поворачиваются и притягиваются заряженным телом. Итак, действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать эти тела по отношению к заряженному телу. Все это можно наблюдать с помощью следующего опыта:

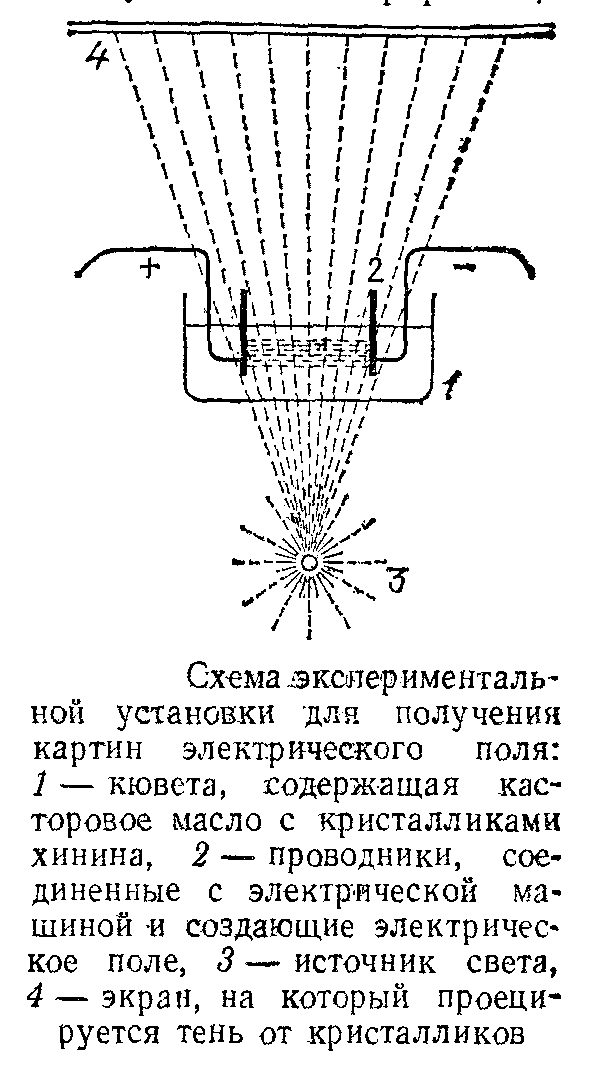Нальем в небольшую стеклянную кювету какой-либо жидкий диэлектрик (например, масло) к которому подмешан порошок с крупинками удлиненной формы (манная крупа в касторовом масле). В кювету поместим, например, две металлические пластинки, и соединим их с электрической машиной, позволяющей непрерывно разделять положительные и отрицательные заряды.

Чтобы удобно было следить за поведением взвешенных в масле крупинок, спроецируем изображение всей картины на экран или просто отбросим тень кюветы на потолок. При заряде пластинок можно видеть, что отдельные крупинки, расположенные вначале совершенно беспорядочно, начинают перемещаться и поворачиваться, и в конце концов устанавливаются в виде цепочек, тянущихся от одного электрода к другому. В этом опыте каждая крупинка подобна маленькой стрелке. Небольшие размеры крупинок позволяют разместить их одновременно во многих точках среды и благодаря этому обнаружить, что действие заряженного тела проявляется во всех точках окружающего пространства.

Таким образом, можно судить о существовании электрического заряда в каком-нибудь месте по действиям, производимым им в различных точках окружающего пространства. В зависимости от заряда и формы заряженного тела действие его в различных точках пространства будет различным. Поэтому для полной характеристики заряда надо знать, какое действие он производит во всевозможных точках окружающего пространства, или, как говорят, надо знать электрическое поле, которое возникает вокруг заряда.

Таким образом, понятием «электрическое поле» мы обозначаем пространство, в котором проявляются действия электрического заряда.

В начале изучения электричества часто возникает стремление объяснить электрическое поле, то есть свести его к каким-либо уже изученным явлениям, подобно тому как тепловые явления мы сводим к беспорядочному движению атомов и молекул. Однако многочисленные попытки подобного рода в области электричества неизменно заканчивались неудачей. Поэтому, как ни крути, электрическое поле есть самостоятельная физическая реальность, не сводящаяся ни к тепловым, ни к механическим явлениям.

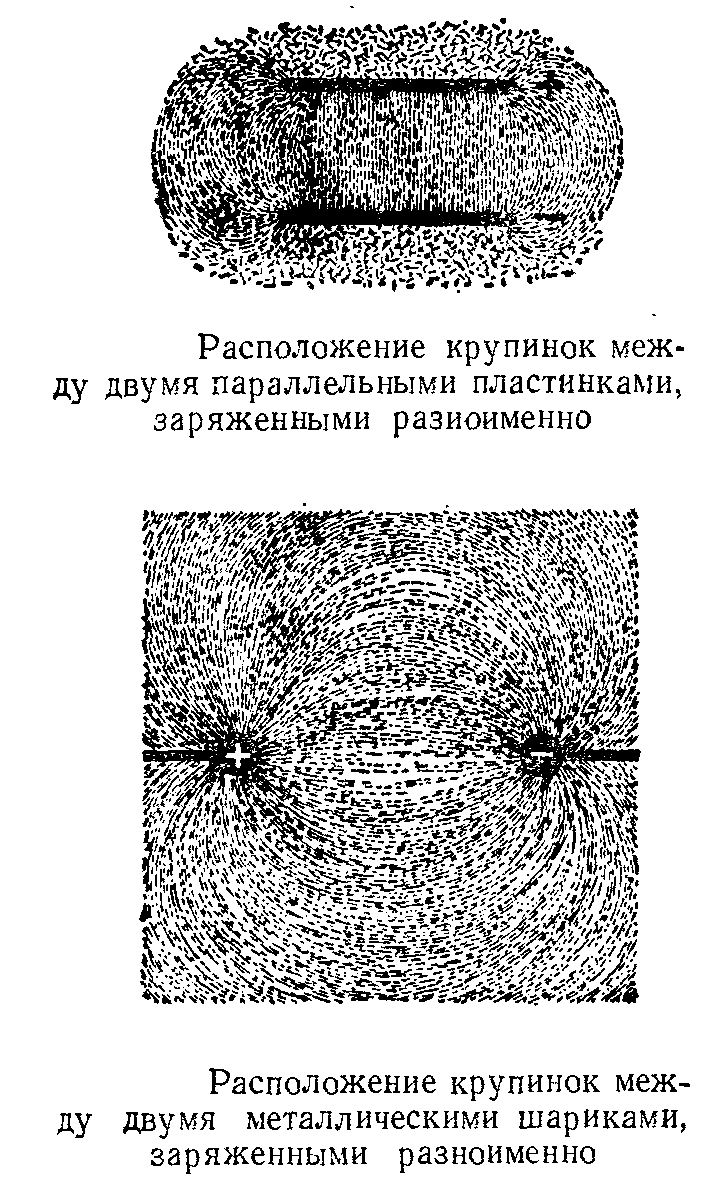Рассмотренный опыт дает лишь качественную картину электрического поля. Для количественной характеристики электрического поля можно использовать любое из производимых им действий. Например, под влиянием электрического поля изменяются оптические свойства некоторых веществ. Это свойство электрического поля можно было бы использовать для количественной оценки поля. Однако, обычно, для этих целей пользуются механическими действиями поля на заряженные частицы.

Представим себе, что электрическое поле создано некоторым зарядом q; внесем в него «пробный заряд» q₀ и измерим действующую на него силу F. Это можно сделать, нанося, например, «пробный заряд» на легкий шарик, подвешенный на шелковой нити и измеряя угол отклонения шарика. По закону Кулона эта сила пропорциональна пробному заряду q₀. Увеличивая этот заряд в 2,3,4 и вообще в n раз, мы будем наблюдать увеличение силы в 2,3,4 или в n раз. Поэтому отношение F/q₀ уже не зависит от пробного заряда q₀ и характеризует только электрическое поле в той точке, где находится пробный заряд. То же имеет место и в любом другом электрическом поле, а не только в поле заряженного шара.

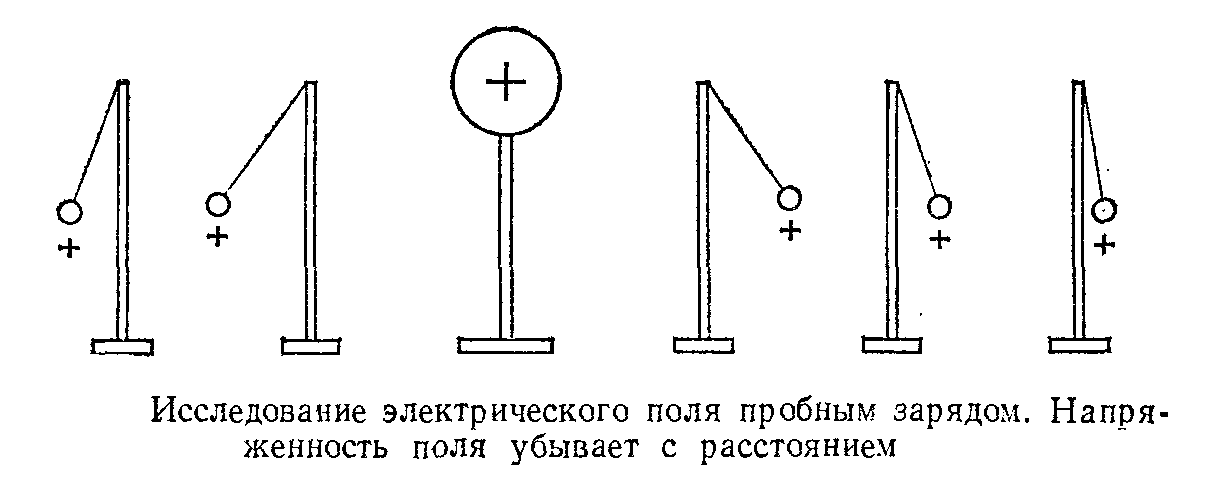
Отношение F/q₀численно равное силе, действующей на единичный заряд, принимают за количественную меру поля и называют напряженностью поля. Таким же образом будет характеризоваться и поле, созданное не одним каким-либо зарядом q, а любой совокупностью зарядов.

Итак, напряженность электрического поля в данной точке пространства есть отношение силы, действующей на заряд, помещенный в точку, к заряду. Следовательно, напряженность поля численно равна силе, действующей на единичный заряд. Если обозначить напряженность поля в некоторой точке через E, заряд, находящийся в этой точке, через q, и силу, действующую на заряд через F, то

E = F/q → F = q∙E.

Напряженность, равная единице, есть напряженность такого поля, в котором на единичный заряд действует сила, равная единице.

В системе СИ за единицу напряженности принимают напряженность поля, в котором на заряд, равный одному кулону, действует сила, равная одному ньютону. Эту единицу называют вольтом на метр (В/м).

Мы определили напряженность электрического поля как физическую величину, численно равную силе, действующей на единичный заряд. Однако всякая сила определяется не только своим числовым значением (модулем), но и направлением. 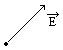Поэтому для полной характеристики напряженности поля надо указать также и ее направление. За направление напряженности поля принимают направление силы, действующей на положительный заряд. Напряженность поля в некоторой точке можно изобразить графически в виде направленного отрезка, исходящего из данной точки, подобно тому, как это делается при изображении силы и других векторных величин.