Вычисление ротора в ДСК
Пусть задана ДСК, в которой вектор 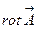 имеет стандартный вид:
имеет стандартный вид:
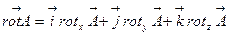
Умножив скалярно это равенство последовательно на орты 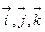 , получим соответствующие проекции на оси ДСК. Так, например, для
, получим соответствующие проекции на оси ДСК. Так, например, для 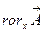 компоненты:
компоненты: 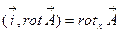 . С другой стороны, умножив уравнение (3.11) на вектор
. С другой стороны, умножив уравнение (3.11) на вектор 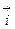 и внося его под знак интеграла, получим
и внося его под знак интеграла, получим
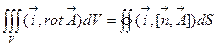 . В поверхностном интеграле сделаем циклическую перестановку в смешанном произведении и обозначим
. В поверхностном интеграле сделаем циклическую перестановку в смешанном произведении и обозначим 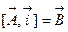 , тогда
, тогда
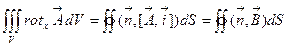 . По формуле Остроградского-Гаусса поверхностный интеграл преобразуем в объемный
. По формуле Остроградского-Гаусса поверхностный интеграл преобразуем в объемный 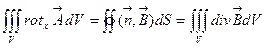
Так как интегрирование ведется по произвольному объему, то подинтегральные функции равны
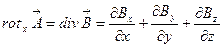 . Нетрудно установить, что
. Нетрудно установить, что
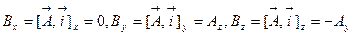 . Следовательно,
. Следовательно, 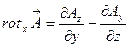
Аналогичные вычисления необходимо провести и для остальных компонент ротора, для чего достаточно подставить в предыдущие формулы соответствующие орты:
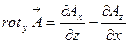 и
и 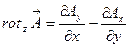 . Окончательно выражение ротора в ДСК будет иметь следующий вид:
. Окончательно выражение ротора в ДСК будет иметь следующий вид: 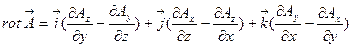 (3.12)
(3.12)
Эту формулу удобно запомнить, если записать с помощью определителя:
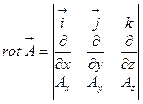 (3.13)
(3.13)
Упражнение 3
1) Вычислить линейный интеграл в плоском векторном поле:
а) 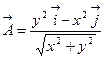 , вдоль полуокружности
, вдоль полуокружности 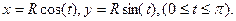
b) 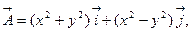 вдоль линии L:
вдоль линии L: 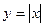 от точки
от точки 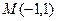 до точки
до точки 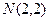 .
.
c) 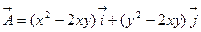 , вдоль параболы
, вдоль параболы 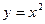 от точки
от точки 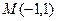 до точки
до точки 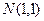 .
.
2) Вычислить работу силового поля 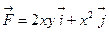 , вдоль дуги окружности
, вдоль дуги окружности 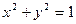 от точки
от точки 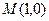 до точки
до точки 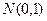 .
.
3) Вычислить линейный интеграл в векторном поле
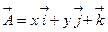 , вдоль витка винтовой линии
, вдоль витка винтовой линии 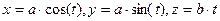 в направлении возрастания параметра
в направлении возрастания параметра 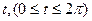 .
.
4) Найти ротор следующих векторных полей:
a) 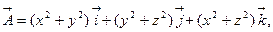
b) 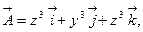
c) 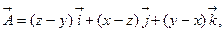
d) 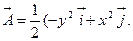
5) Вычислить ротор векторных полей, если 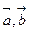 - постоянные векторы,
- постоянные векторы, 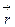 - радиус-вектор:
- радиус-вектор:
a) 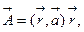
b) 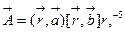
c) 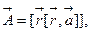
d) 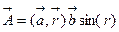
Лекция 4. "Набла" – исчисление
4.1.Операции первого порядка по «набла»
Если посмотреть на пройденный материал, то можно заметить, что до сих пор было введено по сути три новых понятия: градиент скалярного поля, дивергенция и ротор векторного поля. В ДСК они имеют следующий вид:
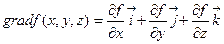 (4.1)
(4.1)
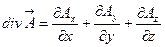 (4.2)
(4.2)
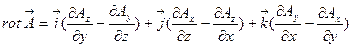 (4.3)
(4.3)
При внимательном рассмотрении системы (4.1)-(4.3) не трудно обнаружить общую закономерность в написании всех трех формул. Эта закономерность становится еще более очевидной, если ввести дифференциальный, векторный опeратор, имеющий в ДСК следующий вид: 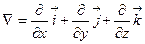 (4.4)
(4.4)
Оператор (4.4) называется "набла"-оператор, или оператор Гамильтона. Его компоненты в ДСК имеют вид 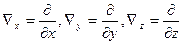 и подчиняются обычным правилам векторной алгебры. С помощью этого оператора систему (4.1)-(4.3) формально можно записать в виде следующих произведений:
и подчиняются обычным правилам векторной алгебры. С помощью этого оператора систему (4.1)-(4.3) формально можно записать в виде следующих произведений: 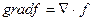 - умножение вектора на скаляр,
- умножение вектора на скаляр,
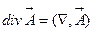 - скалярное умножение двух векторов,
- скалярное умножение двух векторов,
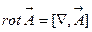 -векторное умножение двух векторов.
-векторное умножение двух векторов.
Такая формальная запись позволяет ввести правила, которые значительно упрощают работу с оператором "набла".
1. Оператор "набла" подчиняется известным правилам векторной алгебры и с ним
Дата добавления: 2016-10-17; просмотров: 1514;
