Вычисление выборочного коэффициента линейной корреляции

При вычислении выборочного коэффициента корреляции выделим случай несгруппированных данных (ихнемного или различные значения количественного признака 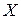и соответствующие им значения признака 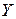наблюдаются по одному разу).

Таблица 6.1

			…
			…

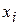
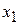
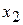
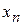
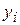
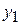
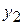
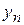
Для вычисления коэффициента корреляции необходимо подставить в формулу (6.1) выражения для выборочных средних

; ;

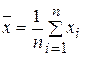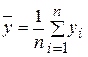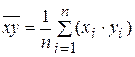
и выборочных средних квадратических отклонений

;

.

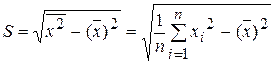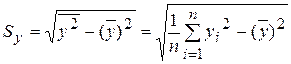Пример 1. В таблице приведен ряд, устанавливающий связь между уровнем 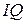и уровнем средней успеваемости учащихся десятого класса.

Таблица 6.2 – Наблюдаемые данные уровня 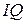и среднего уровня успеваемости по математике у 13-ти школьников десятого класса

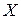- уровень
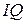
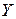- средняя успеваемость	3,1	3,1	3,5	3,7	3,8	4,0	4,2	4,3	4,6	4,7	4,8	4,9	5,0

Существует ли взаимосвязь между уровнем 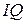(признак 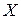) и средним уровнем успеваемости по математике (признак )?

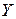Решение

Представим исходные данные в расчетную таблицу.

Таблица 6.3

№ п/п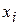
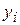
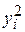
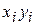
		3,1		9,61	232,5
		3,1		9,61	263,5
		3,5		12,25	315,0
		3,7		13,69
		3,8		14,44
		4,0		16,00
		4,2		17,64
		4,3		18,49	494,5
		4,6		21,16
		4,7		22,09
		4,8		23,04
		4,9		24,01
		5,0		25,00
Суммы		53,7		227,03	6006,5

Вычислим выборочные средние:

; ;

.

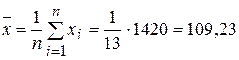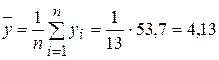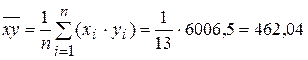Теперь вычислим значения выборочных средних квадратических отклонений:

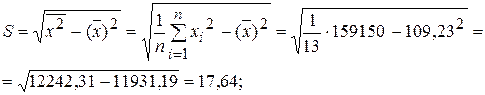
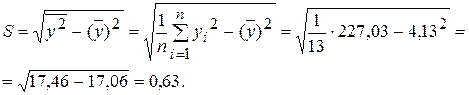
Подставим в формулу:

.

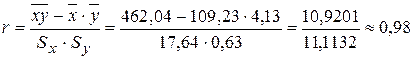Корреляционная связь между уровнем 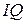и средним уровнем успеваемости по математике близка к линейной положительной. Чем выше уровень 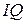у десятиклассников, тем выше средний уровень успеваемости по математике, и наоборот.