Пользоваться правилами векторной алгебры и правилами частного дифференцирования.
Следует сразу подчеркнуть, что применение этих правил требует навыка и, что самое важное, хорошее знание векторной алгебры и дифференциального исчисления. Для закрепления рассмотрим несколько примеров.
1. Вычислить дивергенцию от вектора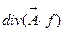 , где
, где 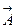 и
и 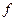 произвольные функции координат. Используя сформулированные выше правила, запишем
произвольные функции координат. Используя сформулированные выше правила, запишем 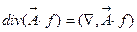 . Справа от оператора
. Справа от оператора 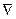 стоит произведение вектора на скаляр, и по правилу дифференцирования произведения мы должны по очереди подействовать оператором на каждый множитель, оставляя другой неизменным:
стоит произведение вектора на скаляр, и по правилу дифференцирования произведения мы должны по очереди подействовать оператором на каждый множитель, оставляя другой неизменным: 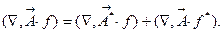
Здесь мы пометили (*) тот множитель, на который неявно действует оператор 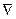 . Чтобы явно
. Чтобы явно
подействовать на соответствующую функцию, применим правила векторной алгебры: в первом слагаемом скалярную функцию 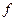 вынесем из-под скалярного произведения, во втором-поменяем местами вектора
вынесем из-под скалярного произведения, во втором-поменяем местами вектора 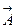 и
и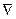 . Тогда
. Тогда 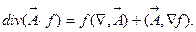 В функциональной форме ответ будет
В функциональной форме ответ будет
иметь следующий вид: 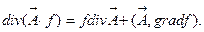
2. Вычислить 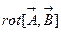 ,где
,где 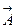 и
и 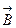 произвольные вектор-функции. Перепишем это выражение в операторной форме
произвольные вектор-функции. Перепишем это выражение в операторной форме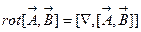 .Мы имеем двойное векторное произведение и, согласно
.Мы имеем двойное векторное произведение и, согласно
правилу дифференцирования произведения, запишем 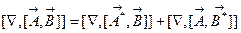 .
.
Здесь, как и раньше, (*) обозначены векторы, на которые неявно действует 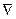 . Раскроем двойное векторное произведение, используя известное векторное правило "ВАС - САВ" [5], тогда,
. Раскроем двойное векторное произведение, используя известное векторное правило "ВАС - САВ" [5], тогда,
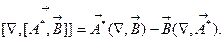 Формальное применение векторных правил привело к нарушению правила дифференцирования произведения, т.к. в первом слагаемом справа вектор
Формальное применение векторных правил привело к нарушению правила дифференцирования произведения, т.к. в первом слагаемом справа вектор 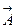 вышел из-под оператора
вышел из-под оператора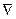 . Исправить это легко, если в скалярных скобках векторы
. Исправить это легко, если в скалярных скобках векторы 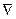 и
и 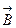 переставить местами, а
переставить местами, а 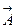 записать справа от них:
записать справа от них: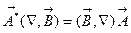 . Таким образом,
. Таким образом,
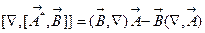 .Аналогичные преобразования справедливы и для слагаемого
.Аналогичные преобразования справедливы и для слагаемого
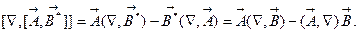 Окончательно будем иметь
Окончательно будем иметь
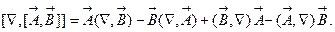 В этом примере мы сталкиваемся с новой дифференциальной операцией, которая в ДСК выглядит очень громоздко:
В этом примере мы сталкиваемся с новой дифференциальной операцией, которая в ДСК выглядит очень громоздко:
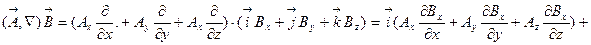
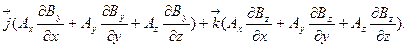 Запишем решение примера 2 в функциональном виде
Запишем решение примера 2 в функциональном виде 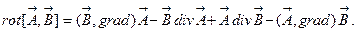
4.2. Операции второго порядка по «набла»
До сих пор рассматриваемые нами дифференциальные операции содержали оператор 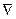 один раз, поэтому их называют операциями первого порядка. Естественно поставить вопрос об операциях второго порядка по
один раз, поэтому их называют операциями первого порядка. Естественно поставить вопрос об операциях второго порядка по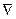 . Для этого построим таблицу, в которой отразим возможные элементарные операции, полученные в результате применения оператора
. Для этого построим таблицу, в которой отразим возможные элементарные операции, полученные в результате применения оператора 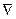 дважды.
дважды.

| 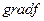
| 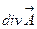
| 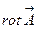
|
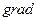
| 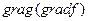 -не существует, т.к. градиент определяется только для скалярного поля -не существует, т.к. градиент определяется только для скалярного поля
| 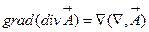 -
элементарная операция второго порядка по -
элементарная операция второго порядка по 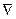
| 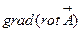 -не сущест- вует, т.к. градиент опре- делен для скаляра -не сущест- вует, т.к. градиент опре- делен для скаляра
|
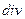
| 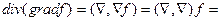
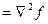 . . 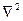 -оператор Лапласа -оператор Лапласа
| 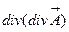 -не существует,
т.к. -не существует,
т.к. 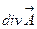 не вектор не вектор
| 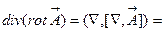
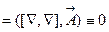
|
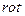
| 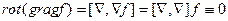
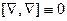 повектор. правилам повектор. правилам
| 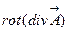 -не существует,
т.к. -не существует,
т.к. 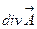 -не вектор -не вектор
| 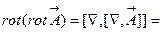
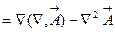
|
Таким образом, из таблицы видно, что фактически существует две элементарные операции второго порядка по 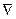 . В ДСК они имеют следующий вид:
. В ДСК они имеют следующий вид:
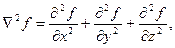
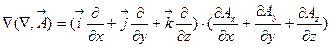 .
.
Следует обратить внимание на то, что две элементарные операции второго порядка всегда тождественно равны нулю – это 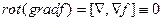 и
и 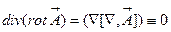
Упражнение 4
1. Вычислить операции второго порядка по "набла":
1) 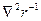 , где
, где 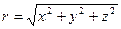
2) 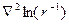 ,где
,где 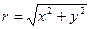
2. Используя правила "набла" исчисления, вычислить: ( 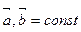 )
)
1) 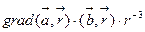 ,
,
2)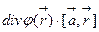 ,где
,где 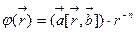
3) 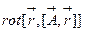 ,где
,где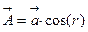
4)& $ grad~(\vec a,\vec r)\cdot (\vec B,\vec a),$ & $\vec B=\vec b\cdot
exp(sin~r),$\\
)& $ div~\vec r(\vec A,\vec a),$ & $ \vec A=[\vec b,\vec r]\cdot~cos~r,$\\
6)& $ rot~[\vec A,\vec r]\cdot (\vec a,\vec r),$ & $\vec A-вектор-функция,$\\
7)& $ grad~(\vec A,\vec B),$ & $\vec A,\vec B$ - вектор-функции\\
8)& $ div~\vec r(\vec A,\vec a),$& $ \vec A=[\vec b,\vec r]cos~r,$\\
9)& $ rot~[\vec a,\vec r](\vec A,\vec r),$ & $\vec A=\vec a\cdot r^{4}$
Дата добавления: 2016-10-17; просмотров: 1142;
