Вычисление двойного интеграла в полярной системе координат
Во многих задачах , требующих применения двойных интегралов, прямоугольная система координат не является наилучшей.
Поэтому следует уметь переходить от одной системы координат к другой , более удобной , например , полярной .
Если 1) подынтегральная функция или 2) уравнение границы области интегрирования В содержит сумму 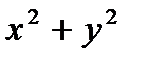 , то в большинстве случаев упрощение интеграла достигается преобразованием его к полярным координатам , т.к. в полярных координатахх.
, то в большинстве случаев упрощение интеграла достигается преобразованием его к полярным координатам , т.к. в полярных координатахх.
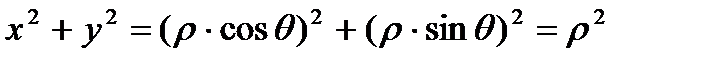 .
.
Рассмотрим , как двойной интеграл в прямоугольных координатах преобразовать в двойной интеграл в полярных координатах.
Пусть имеем двойной интеграл
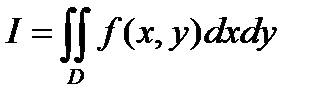 ,
,
где функция f(x,y) непрерывна в замкнутой области D .
Будем считать , что область D такова , что любая прямая , проходящая через начало координат , пересекает границу области более , чем в 2-х точках.
Преобразуем интеграл от прямоугольных координат к полярным координатам r и q .
При выводе формулы преобразования мы воспользуемся , хотя и не вполне строгим ,но простым и наглядным геометрическим методом рассуждений .
Отнесём область D к полярным координатам , приняв ось ОХ за полярную ось , а начало координат за полюс .
В этом случае , как легко установить , прямоугольные координаты точки связаны с полярными координатами следующим соотношениями :
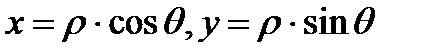
Для того , чтобы получить все точки плоскости ОХУ , достаточно , очевидно, ограничиться знчениями r³ 0 и 0 £q£ 2p.
По определению двойной интеграл
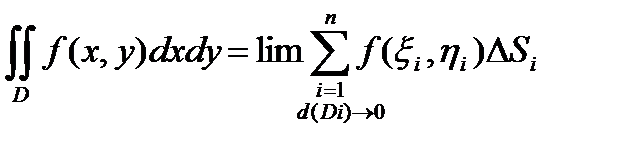 .
.
Поскольку этот предел не зависит от способа разбиения области D на частичные области , то мы можем разбить область D по своему усмотрению.
Рассмотрим такое дробление области D , чтобы легче было осуществить преобразование двойного интеграла к полярным координатам .
Разобъём область D на частичные области с помощью 1) концентрических окружностей с центром в полюсе и 2) лучей , исходящих из полюса О.
Пусть этому разбиению области D отвечает интегральная сумма
( Площади частичных областей Di( i =1,2, . . . , n) обозначим через DSi ).
Частичная область Di представляет собой криволинейную фигуру, ограниченную двумя дугами концентрических окружностей радиусов ri и ri+1 и двумя отрезками лучей .
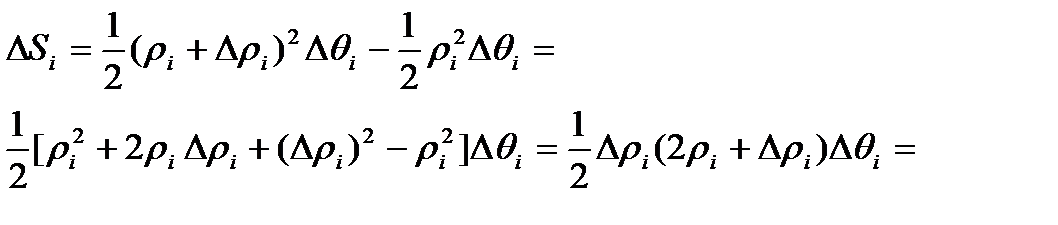
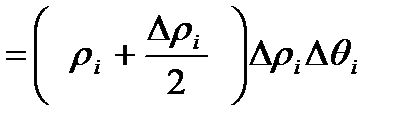 .
.
Обозначим 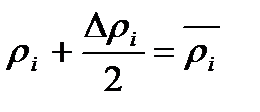 ( Средний радиус между ri и ri+ Dri).
( Средний радиус между ri и ri+ Dri).
Тогда .
Для составления интегральной суммы 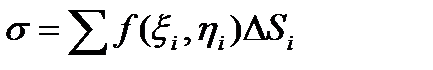 для функции f(x,y) в качестве точек ( xi ,hi ) областей Di выбираем точки , лежащие на средних окружностях радиуса ri .
для функции f(x,y) в качестве точек ( xi ,hi ) областей Di выбираем точки , лежащие на средних окружностях радиуса ri .
Согласно формулам для произвольно выбранной т. ( xi ,hi ) будем иметь
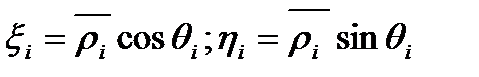
(взяли 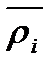 , т.к. точка находится на окружности радиуса
, т.к. точка находится на окружности радиуса 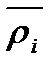 ).
).
Угол qi – между полярной осью и лучом , проходящим через т. ( xi ,hi )
Тогда 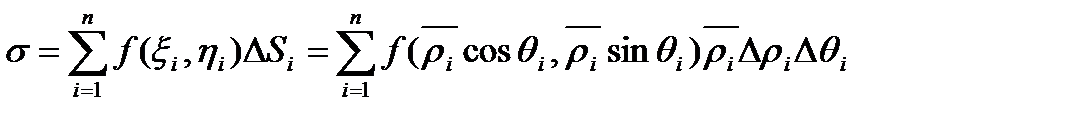
В пределе получим : 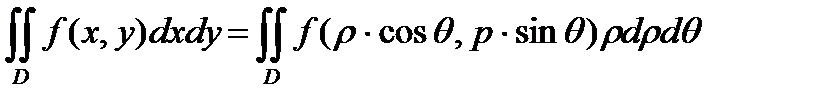
Т.к. слева в равенстве стоит интегральная сумма для непрерывной функции f (x,y) , а справа – интегральная сумма также для непрерывной функции f(rcosq, rsinq)r , то пределы этих сумм существуют и равны соответствующим двойным интегралам .
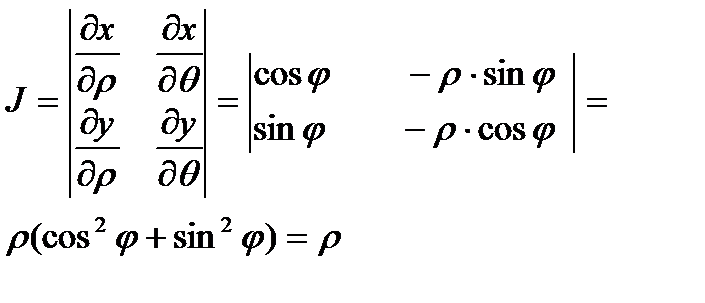
Подставив в сумму получим
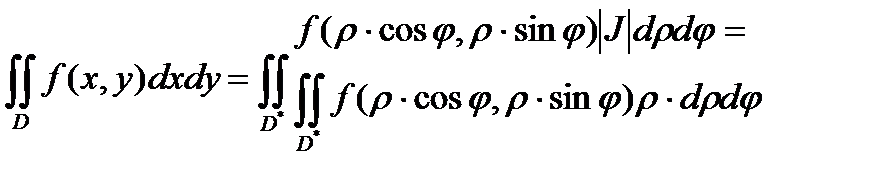 .
.
Его можно сформулировать так :
Правило преобразования .
Для того чтобы преобразовать двойной интеграл в прямоугольных координатах в интеграл в полярных координатах , нужно :
1) в подынтегральной функции f(x,y) заменить х и у соответственно через rcosq и rsinq;
2) элемент площади dxdy в прямоугольных координатах заменить произведением rdrdq( которое называют элементом площади в полярных координатах ).
Сначала отмечают крайние значения a и b полярного угла q .
Угол a соответствует точке А , угол b – точке В контура . точки А и В разбивают контур ( границу области D) на 2 части : АСВ и ВЕА, уравнения которых соответственно обозначают через r1 = r1( q ) и r2 = r2( q ) , где r1( q ) и r2( q ) – непрерывные функции , заданные на сегменте [a,b] . Следовательно, область D ограничена 1) линиями
r1 = r1( q ) – уравнение АСВ,
r2 = r2( q ) – уравнение ВЕА и
2) двумя лучами , образующими с полярной осью углы a и b ; причём a<b ; r1( q ) и r2( q ) – непрерывные функции .
Следовательно , пределы внешнего интеграла будут a и b . Найдём пределы внутреннего интеграла .Для этого фиксируем произвольное значение угла q между a и b , затем из полюса О под углом q проводим луч ОЕ.
Точка входа этого луча в области D лежит на линии r1 = r1( q ) , а точка выхода его из области D лежит на линии r2 = r2( q ) .
Уравнения этих линий и дают соответственно нижний и верхний пределы внутреннего интеграла :
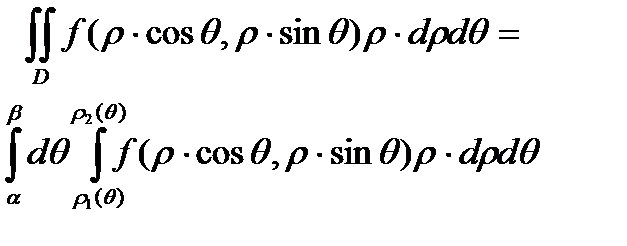 . (
. (
Пример 6.8.7.
Перейти к полярным координатам и расставить пределы интегрирования в следующем интеграле :
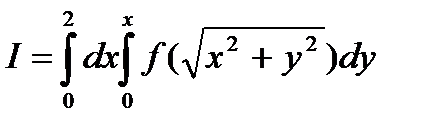 .
.
Решение
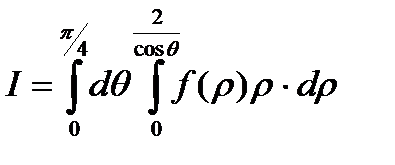
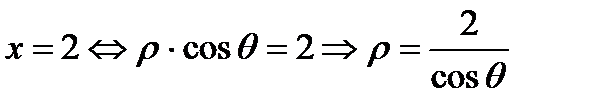 .
.
Пример6.8.8.Вычислить двойной интеграл 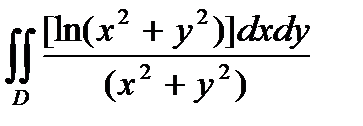 ,
,
где область D есть кольцо , заключенное между окружностями х2 + у2 = е2 и х2 + у2 = 1 .
y
x
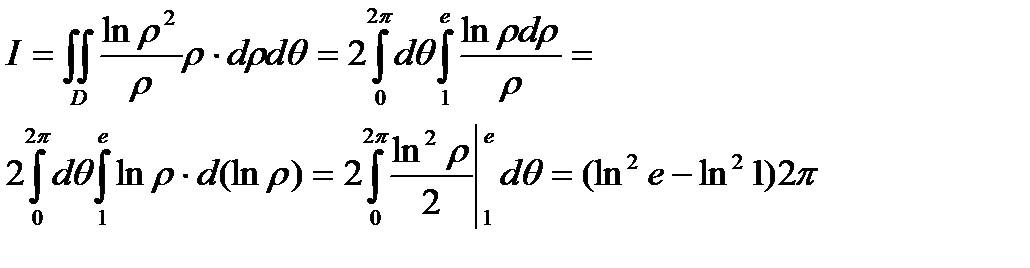
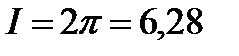
Пример 6.8.9.Вычислить 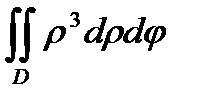 , где (D) область , ограниченная полярной осью и кривой
, где (D) область , ограниченная полярной осью и кривой 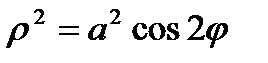 с дополнительным условием : полярный угол
с дополнительным условием : полярный угол 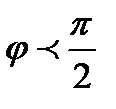 .
.
Решение .
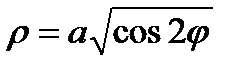
Кривая 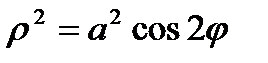 - лемниската . Определим , как изменяется угол j в области D . С увеличением угла j ( при условии j<p/2) полярный радиус r уменьшается . При некотором значении j он становится равным нулю . Найдём это значение j .
- лемниската . Определим , как изменяется угол j в области D . С увеличением угла j ( при условии j<p/2) полярный радиус r уменьшается . При некотором значении j он становится равным нулю . Найдём это значение j .
Подставим в уравнение лемнискаты r = 0 и получим уравнение для определения j :
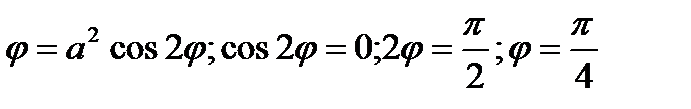
( учтено условие , что j<p/2 ).
Таким образом , в области D полярный угол изменяется от 0 до p/4 .
Переменная r изменяется в области D от r= 0 до 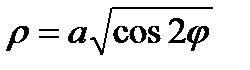 , по формуле
, по формуле
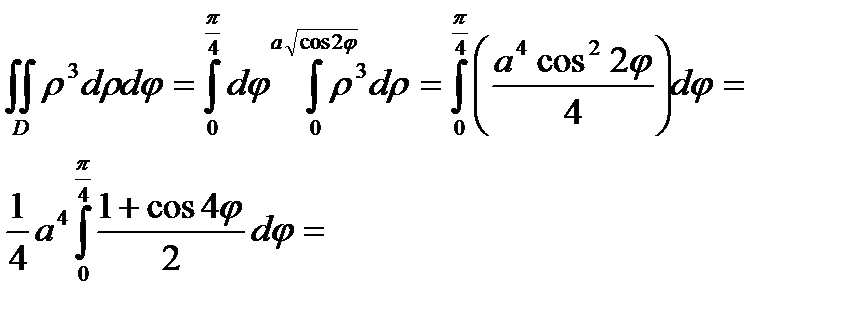
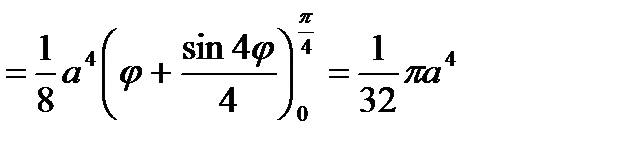 .
.
Дата добавления: 2016-10-17; просмотров: 1705;
