Свойства двойного интеграла

Двойной интеграл обладает рядом простейших свойств , вполне аналогичных соответствующим свойствам простого интеграла .

Доказательство основных свойств двойного интеграла ( подобно доказательству свойств простого интеграла ) основано на его определении как предела интегральной суммы .

1. Двойной интеграл по области D от алгебраической суммы функций равен алгебраической сумме интегралов слагаемых по той же области .

Так для двух функций это свойство запишется следующим образом :

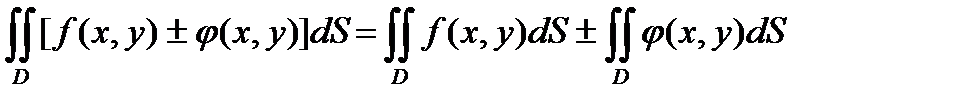
3.Если область D разбита на 2 области D₁ и D_II без общих внутренних точек , а функция f(x,y) непрерывна во всех точках области D , то :

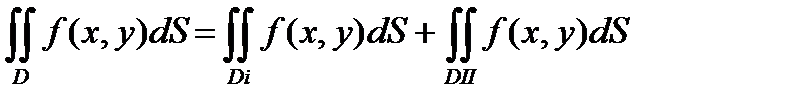
4. Если f(x,y) и j(x,y) – интегрируемые в области D функции , то из неравенства

f(x,y) £j(x,y) , ( x,y)ÎD

следует неравенство

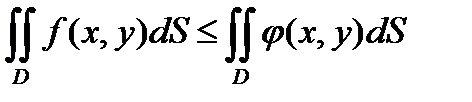
(другими словами , неравенство можно почленно интегрировать !!)

5 . Если функция f(x,y) интегрируема в области D , то и функция f(x,y) интегрируема в этой области и

ï 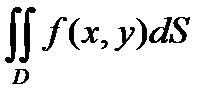ï£ ôf(x,y)ôdS.

-ïf(x,y) ï£ïf(x,y)ï£ïf(x,y)ï ,

получим

- .

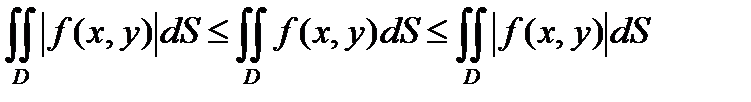
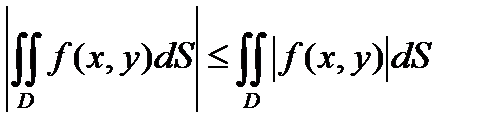Доказано , если -а £ х £ а , тоô х ô£ а .