Рівняння методу Треффца. Приклад. Порівняння основних підходів
Система рівнянь методу Треффца

У методі Треффца функції 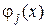 обираються таким чином, щоб кожна з них являла собою частинний розв’язок диференціального рівняння Ейлера варіаційної задачі
обираються таким чином, щоб кожна з них являла собою частинний розв’язок диференціального рівняння Ейлера варіаційної задачі
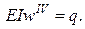
Для нашого прикладу (рис. 11.1) отримаємо
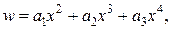
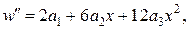
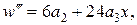
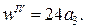
Ураховуючи, що 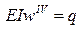 ,
,
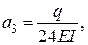
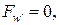
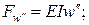
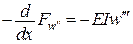 .
.
Тоді
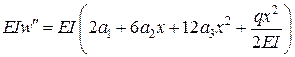 ,
,  .
.
Система рівнянь методу Треффца.

Розв’язок системи дає

 .
.
Підсумкова таблиця
| Метод Рітца | Метод Бубнова-Гальоркіна | Метод Треффца | |
| Як задається ф-ція w? | 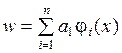
| 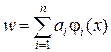
| 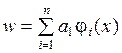
|
Як обираються
функції 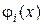 ? ?
| Функції 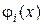 задовольняють частині граничних умов. Задоволення усім граничним умовам
не є обов’язковим задовольняють частині граничних умов. Задоволення усім граничним умовам
не є обов’язковим
| Функції 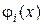 обираються так, що задовольняють усім граничним умовам обираються так, що задовольняють усім граничним умовам
| Функції 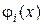 є частинними розв’яз-ками диференціаль-ного рівняння Ейлера є частинними розв’яз-ками диференціаль-ного рівняння Ейлера
|
Як знаходяться невідомі
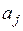 ? ?
| Із умови екстремуму функціоналу
 , ,
 , ,
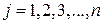
| Із умови ортогональності кожної функції 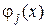 лівій частині диферен-ціального рівняння Ейлера задачі лівій частині диферен-ціального рівняння Ейлера задачі
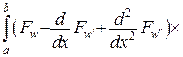


| Із умови ортого-нальності кожної функції 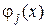 лівій частині диферен-ціального рівняння Ейлера задачі на границі області лівій частині диферен-ціального рівняння Ейлера задачі на границі області
 
|
Лекція 13
Дата добавления: 2016-12-26; просмотров: 671;
