ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Задача 10.1. Найти энергию системы двух точечных зарядов q₁ и q₂, расположенных на расстоянии r друг от друга.

Энергия связи определяется как работа поля, которая будет совершена силами поля над системой зарядов при удалении их друг от друга на такое расстояние, на котором взаимодействием между зарядами можно пренебречь, то есть на бесконечно большое расстояние.

Заметим, что в случае одноименных зарядов энергия связи положительна, а в случае разноименных – отрицательна.

Вернемся к задаче.

Решение. Найдем энергию связи двух точечных зарядов q₁ и q₂ (рис. 10.1). Закрепим заряд q₁. Тогда потенциал поля, созданного зарядом q₁ в точке 2 – той, где находится заряд q₂, равен

.

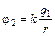Работа по перемещению заряда q₂ из точки 2 на бесконечность равна

.

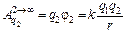Эта работа и равна искомой энергии.

Ответ:

. (10.1)

СТОП! Решите самостоятельно: А1, А2, А5.

Задача 10.2. Найти энергию связи системы из трех точечных зарядов q₁, q₂, q₃, если расстояния между зарядами равны: r₁₂, r₁₃, r₂₃ (рис. 10.2).

q1, q2, q3 r12, r13, r23	Решение. Будем по очереди удалять заряды и вычислять работу, которую совершает при этом поле. Удаляем первый заряд. Потенциал в точке 1, созданный зарядами q2 и q3, равен . Тогда работа по удалению на бесконечность .
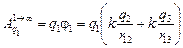W = ?
Рис. 10.2

Удаляем второй заряд. Потенциал в точке 2, созданный зарядом q₃, равен

.

Тогда работа по удалению на бесконечность

.

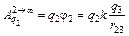Общая работа поля равна

.

Ответ: .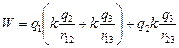

СТОП! Решите самостоятельно: С1, С3.

Задача 10.3. Система состоит из точечных зарядов q₁, q₂, …, q_n. Потенциал в точке нахождения i-го заряда, созданного полем всех остальных зарядов, равен

.

Доказать, что энергия связи этой системы равна

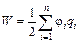. (10.2)

Решение. Докажем, что формула (10.2) справедлива для п = 2 (рис. 10.3). Запишем потенциалы:

; .

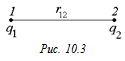
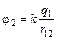Тогда

.

Таким образом, для п = 2 формула (10.2) доказана.

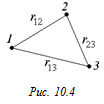Докажем, что формула (10.2) справедлива для п = 3 (рис. 10.4). Запишем потенциалы:

; ;

.

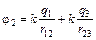Заметим, что энергия связи не может зависеть от того, в какой последовательности мы удаляем заряды. Иначе удаляя заряды в одной последовательности, а возвращая их обратно в другой, мы получили бы «бесплатную» работу.

Итак, удаляем последовательно первый и второй заряды, а третий заряд оставляем. Тогда согласно решению задачи 10.2 энергия связи

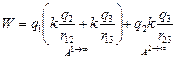. (1)

Теперь удаляем третий и второй заряды, а первый оставляем на месте:

. (2)

Сложим почленно уравнения (1) и (2):

.

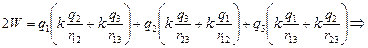
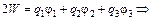
Формула (10.2) доказана.

Можно провести подобное доказательство и для произвольного п, попробуйте сделать это самостоятельно.

Задача 10.4. Вычислить энергию поля равномерно заряженной сферы заряда Q и радиуса R.

Q R	Решение. Разобьем сферу на п малых участков, заряд каждого из которых qi. Тогда (рис. 10.5). Потенциал поля в любой точке сферы . Тогда согласно формуле (10.2) 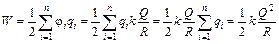. Ответ:
W = ?
Рис. 10.5

. (10.3)

СТОП! Решите самостоятельно: В4, В6, В7.

Задача 10.5. Четыре одинаковых заряда q находятся в вершинах квадрата со стороной а (рис. 10.6). Найти энергию системы.

q а	Решение. В силу симметрии задачи потенциалы всех вершин равны: 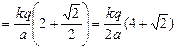.	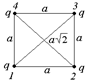Рис. 10.6
W = ?

Согласно формуле (10.2)

.

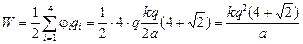Ответ: .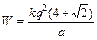

СТОП! Решите самостоятельно: В8.

Задача 10.6. Найти энергию поля, созданного системой из четырех зарядов q, расположенных в вершинах тетраэдра со стороной а (рис. 10.7).

q а	Решение. В силу симметрии задачи потенциалы всех вершин тетраэдра равны: .
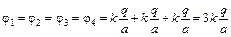W = ?

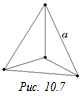Согласно формуле (10.2)

.

Ответ: .

СТОП! Решите самостоятельно: С4.

Задача 10.6. Энергия равномерно заряженной квадратной пластины со стороной а равна W₀. Чему равна энергия квадратной равномерно заряженной пластины со стороной 2а, если поверхностная плотность заряда пластин одинакова?

а 2а W0	Рис. 10.8	Решение. Читатель: Поскольку вторая пластина состоит как бы из четырех пластин со стороной а, то ее энергия должна быть в 4 раза больше: W = 4W0.
W = ?

Автор: Не совсем так. Вы не учли, что четыре пластины, из которых состоит одна большая, отталкиваются друг от друга. Если мы разрежем большую пластину на четыре маленьких и предоставим их самим себе, то они разлетятся на бесконечное расстояние. При этом силы электрического отталкивания совершат работу, которая перейдет в кинетическую энергию пластин. А потенциальная энергия каждой маленькой пластины при этом сохранится. Ясно, что энергия большой пластины должна быть больше 4W₀.

Представим пластины состоящими из большого числа точечных зарядов q_i, расположенных в определенном порядке. Расстояние между i-м и j-м зарядами равно r_ij. Тогда энергию пластины 1 можно записать в виде

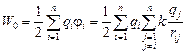. (10.4)

Будем теперь постепенно «превращать» пластину 1 в пластину 2. Для этого все размеры пластины увеличим в 2 раза (а заряды добавлять не будем). Тогда расстояние между любыми двумя зарядами q_i и q_j увеличится в 2 раза. Каждый потенциал j_i уменьшится в 2 раза, а значит, общая энергия W¢ уменьшится в 2 раза: W¢ = W₀/2.

Теперь, чтобы плотность заряда s = q/S нашей пластины стала такой же, какой она была вначале, увеличим величину каждого заряда q_i в 4 раза (так как площадь S увеличилась в 4 раза). Тогда согласно формуле (10.4) каждый потенциал увеличится в 4 раза, а каждое произведение q_ij_i увеличится в 4×4 = 16 раз! Следовательно, энергия W¢ увеличится в 16 раз:

.

Ответ: W = 8W₀.

СТОП! Решите самостоятельно: С7, С8.