Электростатическая индукция

Это явление состоит в том, что под действием внешнего поля заряды внутри сплошного проводника перераспределяются. Причем перераспределяются они всегда так, что созданное ими (после перераспределения) поле в сумме с внешним полем всегда равно нулю внутри проводника. То есть наведенное «внешним» полем «внутреннее» поле всегда «гасит» это внешнее поле.

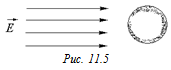Задача 11.3. Незаряженный металлический шар поместили в однородное электростатическое поле (рис. 11.5). Как изменилась при этом картина силовых линий? Будет ли шар двигаться или останется неподвижным?

Решение. Под действием электростатического поля электроны сместятся влево, а в правой части сферы образуется избыток положительных зарядов (рис. 11.6) При этом поле внутри сферы будет отсутствовать, а поверхность сферы будет эквипотенциальной. Следовательно, силовые линии должны быть перпендикулярны к поверхности сферы (рис. 11.7).

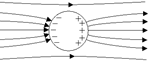Рис. 11.7 Рис. 11.8

Внешнее поле будет действовать на положительные и отрицательные заряды, скопившиеся в разных частях шара с равными по величине и противоположными по направлению силами (рис. 11.8), поэтому шар ускоряться не будет: .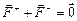

Задача 11.4. В каком направлении будет ускоряться незаряженный металлический шар, помещенный в неоднородное электростатическое поле (рис. 11.9)?

Рис. 11.9 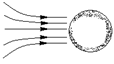Рис. 11.10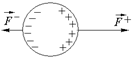

Решение. Поле слева сильнее, чем поле справа (рис. 11.10), поэтому шар будет втягиваться в область более сильного поля, т.е. в ту область, где напряженность по величине больше.

СТОП! Решите самостоятельно: А4, А14, В1, В4, В5, С7–С9.

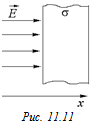Задача 11.5. В однородном поле, модуль напряженности которого равен Е, поместили бесконечную металлическую пластину с суммарной поверхностной плотностью заряда s > 0 (рис. 11.11). Линии напряженности внешнего поля перпендикулярны к поверхности пластины. Найти плотности зарядов s₁ и s₂ на ее поверхностях, а также значения проекций вектора напряженности результирующего поля слева и справа от пластины.

Е s	Решение. Положим для определенности s1 > 0 и s2 > 0, т.е. будем считать, что на левой и правой поверхностях пластин будут положительные заряды (рис. 11.12). Ясно, что здесь s1 < s2, так как внешнее поле «отодвигает» положительные заряды к правой стороне пластины.
s1, s2 = ? = ? = ?

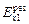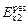Общая плотность поверхностных зарядов при этом не изменится:

s₁ + s₂ = s. (1)

Каждая поверхность пластины создает свое электрическое поле: левая 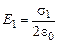, правая 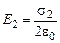. В сумме с внешним полем они внутри пластины «дают» ноль:

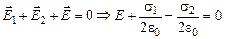. (2)

Решая систему из уравнений (1) и (2) относительно неизвестных s₁ и s₂, получим

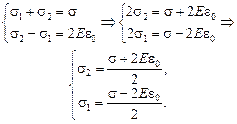
Как видим, величина s₂ всегда положительна, а величина s₁ может быть как положительной, так и отрицательной: если s > 2Еe₀, то s₁ > 0, а если s < 2Еe₀, то s₁ < 0. Другими словами, в слабом поле обе поверхности пластины будут иметь положительный заряд, а в сильном внешнем поле левая сторона пластины будет заряжена отрицательно.

Теперь найдем результирующее поле слева и справа от пластины. Введем ось х (рис. 11.13) и запишем величину проекции напряженности результирующего поля на ось х как сумму проекций напряженности поля пластины 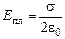и внешнего поля Е.

Слева от пластины:

;

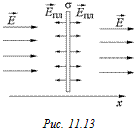
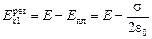справа от пластины:

.

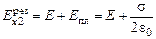Ответ: ; ;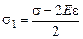

; .

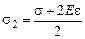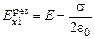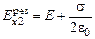СТОП! Решите самостоятельно: С10–С12.