Индукция как вывод и индукция как метод

Следующей важной линией развития классической индукции явилось различение ее как метода и как вывода. Впервые достаточно четко это осуществил Аристотель. С одной стороны, он трактует индукцию как метод опытного познания, как путь движения мысли от чувственно-воспринимаемого единичного к общим понятиям и утверждениям. С другой стороны, он впервые исследовал индуктивный способ движения мысли со стороны его логической формы, а именно как вывод, как специфичный тип рассуждения.

Индукцию, как вывод, делят на:

- материальную,

- формальную.

Формальная индукция - это индукция, как вывод только с точки зрения ее логической формы, без всякой связи с содержанием посылок индукции, от которого полностью отвлекаются. Материальная индукция - это рассуждение (вывод) от частного к общему с учетом не только его алогической формы, но и его содержания.

Когда в науке говорят об индуктивных выводах, то, как правило, имеют в виду именно материальную индукцию как логический способ движения научно-исследовательской мысли от опыта к теории, как при получении новых научных законов путем обобщения опытных данных, так и при обосновании имеющегося научного знания эмпирическим путем.

Благодаря различению формальной и материальной индукции Д. С. Миллю удалось четко сформулировать главную тайну индукции: «Почему в иных случаях единичного примера достаточно для полной индукции, тогда как в других даже мириады согласных между собой примеров, при отсутствии хотя бы одного исключения, известного или предполагаемого, так мало дают для установления общего предположения? Всякий, кто может ответить на этот вопрос, ближе знает философию логики, чем мудрейший из древних философов: он разрешил проблему индукции».

Среди видов материальной индукции различают научную и ненаучную индукции. Первая в отличие от второй опирается в своих посылках не на всякие, а только на существенные свойства и отношения, благодаря чему достоверность ее заключений (индуктивных обобщений) имеет доказательный характер, хотя по логической форме она представляет собой пример неполной индукции. Тогда как доказательность любых дедуктивных выводов не зависит от содержания посылок, а только от их логической формы, для многих индуктивных выводов имеет место обратное. Здесь учет содержания посылок и, в частности, учет релевантности и существенности заключенной в них информации имеет первостепенное значение для оценки правильности и доказательности сделанных индуктивных заключений. Это говорит о том, что между свойствами дедуктивных и индуктивных выводов нет полной симметрии. В отличие от дедукции индукция является существенно содержательно-логической операцией.

В этой связи хотелось бы особо выделить принцип логического плюрализма, имеющий первостепенное значение для потенциальных разработчиков индуктивных программ. Приведем его в виде тезисов.

Тезис 1. Средства формализации «не накладываются» на задачу, а порождаются семантикой задачи («если для решения данной задачи нет адекватных формальных средств, то их следует выдумать »).

Тезис 2. Сфера прикладных логических исследований подобна физике - эксперимент может доставлять новые феномены, формальное описание которых есть творческая задача, могущая привести к разработкам новых формальных аппаратов и понятий. Открытие и описание новых фигур формального рассуждения - путь аппроксимации эвристики. Таким образом, множества логических формализмов расширяется в связи с появлением таковых задач имитации рассуждении, требующих адекватных средств формализации.

Тезис 3. В зависимости от природы воспринимаемой компьютером ситуации (и соответствующих рассуждении, необходимых для обработки данных) должна выбираться подходящая формальная система с соответствующей логикой, имитирующая рассуждения как адекватные реакции на воспринимаемую информацию (например, использование неклассических логик для обработки данных с неполной информацией).

Приведем некоторые примеры формализации индукции как вывода. Рассматривая интерпретацию законов Д. С. Милля в рамках исчисления высказываний, можно получить следующие правила вывода:

Здесь а, b, х, у, z, w могут обозначать не только переменные, но и любые формулы. Следует отметить, что применение правил (1) - (3) может в принципе приводить к противоречиям, т. е. из некоторых наборов данных могут выводиться как утверждения х =>у, так и х =>Øy. Однако в этом нет ничего противоестественного, так как подобные противоречия являются отражением реальных противоречий, существующих в экспериментальных данных. В этом плане все выводы, полученные по приведенным выше правилам, есть гипотезы, достоверность которых должна быть оценена тем или иным способом.

Интерпретация законов Д. С. Милля в рамках расширенного языка логики предикатов привела к созданию одного из наиболее ярких и интересных методов - ДСМ-метода автоматического порождения гипотез в ЭС с неполной информацией. Этот метод предназначен для выявления причинно-следственных эмпирических зависимостей на множестве нечисловых фактов в условиях неполноты информации.

Индукцию как метод можно рассматривать как процесс рассуждения, в котором взаимодействуют между собой не только специфические индуктивные правила вывода или операции, но и другие логические приемы. Перечислим основные операции индуктивного метода:

· генерализация (обобщение);

· специализация (конкретизация);

· рассуждение по аналогии;

· поиск контрпримера;

· тестирование результатов, полученных с помощью индукции, на новых данных.

Можно считать, что поиск закономерностей включает отдельные акты выявления сходства, различия, сопутствующих изменений. Так, в основе многих алгоритмов распознавания образов лежит поиск общности между объектами одного класса и различий между объектами разных классов. Разделяющие функции, двоичные деревья, минимальные тесты, кластеры и т. д. - это все формальные, легко программируемые методы поиска общностей и различий. При этом, если в подходах, основанных на поиске разделяющей плоскости, .идея поиска общностей и различий выражается в том, что объекты одного класса лежат по одну сторону, а разных - по различные стороны разделяющей плоскости, то в ряде других подходов следование методам Милля просле­живается и в работе алгоритмов. Например, некоторые алгоритмы распознавания образов и формирования понятий основаны на обобщении информации об объектах, осуществляемой путем пересечения описаний объектов одного класса. Пересечение описаний объектов с целью формирования признаков класса или понятий фактически представляет собой следование методу сходства.

Существуют и алгоритмы, явно следующие методу различия. Так, в системе Уинстона формирование понятий о сценах производится путем сравнения граф-описания сцены, соответствующей понятию, с граф-описанием сцен, являющихся контрпримерами к понятию. В результате такого сравнения в граф-описание понятия вводятся описания различий сравниваемых сцен.

На методе сопутствующих изменений основан ряд алгоритмов восстановления функций, таких, как ЭМП-2, и отбора признаков изменения явлений.

Среди алгоритмов таксономии, также основанных на выявлении «близости» (похожести, сходства) объектов из одного таксона и «удаленности» (различия) объектов из разных таксонов, можно выделить алгоритм ФОРЭЛЬ.

Следует, однако, отметить, что для поиска закономерностей, наряду с общими индуктивными методами, необходима совершенная система представления знаний конкретных проблемных областей.

Индукция как метод лежит в основе направления, получившего название индуктивного формирования понятий. Под понятием понимается обобщенная информация о множестве объектов, представленных наборами значений признаков, которая:

- отображает характерные для этого множества логические отношения между отдельными значениями признаков;

- является достаточной для различения с помощью некоторого правила распознавания объектов, принадлежащих множеству, от объектов не принадлежащих ему.

Обобщенная информация, служащая понятием, может быть представлена выражением некоторого языка или структуры данных в памяти компьютера или человека. Слово «обобщенная» в данном случае означает, что понятие включает лишь существенные значения признаков, характеризующие множество объектов в целом, и не включает некоторые частные значения признаков, индивидуализирующие отдельные объекты.

Множество объектов, которому соответствует понятие, называется объемом понятия. В зависимости от того, входит или не входит объект в объем некоторого понятия, его называют положительным или отрицательным.

Здесь следует особо отметить работу по моделированию способности человеческого мозга к формированию абстрактных понятий. Э. Ханг рассматривает некоторое «разумное» устройство (включая человека) как некую систему, способную приспосабливаться к окружающей среде. Для такого приспособления устройство должно уметь непрерывно классифицировать мало отличающиеся состояния среды как одинаковые или неодинаковые. Конкретные пути классификации могут меняться от случая к случаю: один раз мы можем китов объединить с медведями, а другой раз - с акулами. Процесс формирования понятий понимается Э. Хангом как способность «разумного» устройства вырабатывать правила классификации на основе собственного опыта. Само же устройство, способное к такой деятельности, получило название системы формирования понятий (Concept Learning System) или сокращенно CLS. Такая система была построена, т. е. создана компьютерная программа, осуществляющая некоторые операции над символами.

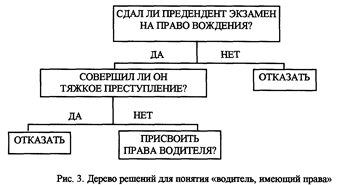
Для того чтобы было понятно, о чем идет речь, приведем следующий пример процесса формирования понятия «водитель, имеющий права».

Предположим, что всех людей, обращающихся за удостоверением на право вождения автомобиля, можно описать с помощью следующих признаков: пол (м, ж), возраст (молодой, совершеннолетний, средний, пожилой), судимость (к суду не привлекался, привлекался по мелкому делу, совершал тяжкое преступление), водительские навыки (сдал экзамен, не сдал экзамен). Правило присвоения квалификации состоит в следующем: любое лицо, которое не совершило тяжкого преступления и сдало соответствующий экзамен, получает официальный статус «водителя». Понятие «водитель, имеющий права», можно представить следующим образом:

S =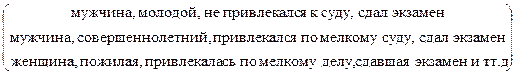

В матрице S отсутствуют только те описания, которые содержат характеристики (т. е. значения признака) "совершил тяжкое преступление" или «не сдавший экзамен». Значительно проще представить это понятие как правило последовательного поиска решения (рис. 3). Такие правила (в виде последовательности вопросов) Э. Хает называет деревьями решений.

Процесс формирования понятий должен содержать стадии, необходимые для индуктивного метода. Рассматривая проблему индукции в математике, Д. Пойа выделил следующие этапы:

ff) оценка имеющейся информации с тем, чтобы на ее основе сформировать гипотезу; эта гипотеза должна соответствовать известным фактам и по возможности оставаться верной применительно к новым данным;

gg)получение новых данных;

hh)проверка работоспособности гипотезы по отношению к этим новым данным, если она оказывается неверной, снова оценить всю совокупность имеющихся данных и предложить на их основе новую гипотезу.

Формирование понятий в системе CLS происходит с учетом приведенных выше этапов. Среди методов формирования понятий особо следует выделить алгоритм, где формирование понятий осуществляется с помощью специально введенного формализма - растущей пирамидальной сети (a-рис).