Методы индуктивного вывода

Виды индукции

Под классической индукцией понимается способ движения мысли от частного к общему, от знания менее общего к знанию более общему. Исторически сложились три ее различных вида:

1) перечислительная или энумеративная индукция (полная и неполная);

2) элиминативная индукция (схемы установления причинно-следственных связей между явлениями);

3) индукция как обратная дедукция (рассуждения от следствий к основаниям).

Впервые логически обосновали содержание индукции древнегреческие философы: индукцию как обратную дедукцию - Сократ и Платон, перечислительную индукцию - Аристотель, элиминативную - эпикурейцы. Дальнейшее логическое развитие понятия индукции шло по линии конкретизации и уточнения выделенных видов, причем в разные исторические эпохи преимущественное значение получал один из ее видов:

перечислительная индукция - Древняя Греция и средневековье; элиминативная индукция - Новое время (Ф. Бэкон) и XIX в. (Гершель, Милль); индукция как обратная дедукция - XVIII в. (Ньютон), вторая половина XIX в. (Уэбелл, Джевонс).

Для XX в. характерно внимание ко всем видам индукции, и, прежде всего в плане их более точной логической экспликации. В схематическом виде эта линия развития индукции изображена на рис. 1.

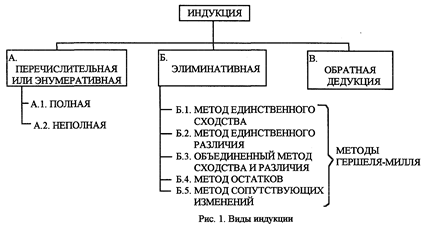
А. Энумеративную индукцию Ф. Бэкон назвал "индукция через простое перечисление, в котором не встречается противоречащего случая". Например, наблюдая, что отдельные слоны едят с помощью хобота, мы можем по неполной индукции сделать заключение, что «все слоны едят с помощью хобота». Следующие два примера поясняют разницу между полной и неполной индукцией.

Пример 1. Первая ворона - черная, вторая ворона - черная... Все НАБЛЮДАЕМЫЕ вороны - черные. Пример 2. Первая ворона- черная, вторая ворона - черная... ВСЕ вороны черные. Полная индукция через простое перечисление подразумевает выделение конечного класса объектов, неполная - предполагает бесконечное число объектов данного класса. Исследуя индукцию через перечисление как специфическую форму умозаключения, Аристотель различал силлогистическую и несиллогистическую индукции, впоследствии получивших название полной и неполной. Только полная индукция рассматривалась Аристотелем как формально законный вид вывода. Энумеративную индукцию (неполную) анализировал Б. Рассел, которому принадлежит простое и изящное доказательство ее несостоятельности в качестве чисто логического принципа.

Очень часто в современной литературе неполную индукцию через простое перечисление рассматривают как способ формирования некоторой гипотезы. Заключение (обобщение в виде общего суждения) берется как гипотеза, догадка, которую в ходе последующего исследования надлежит или более строго обосновать, или оценить, или опровергнуть. Как можно оценивать гипотезы? Один из самых распространенных способов - это применение методов математической статистики. Направление работ в этой области получило название «вероятностной индукции».

Другое направление, «структурная индукция», связано с использованием логик. Деление это весьма условно. К настоящему времени осуществлен симбиоз статистики и логики при создании метода автоматического образования гипотез - GUHA.

Теперь обсудим роль контрпримеров для обобщений (гипотез), сделанных в результате научных исследований. Представим ситуацию, когда первый эксперимент показал результат, который гипотеза считала невозможным. Что делают в этом случае? Существует точка зрения, что несогласующийся с гипотезой эксперимент опровергает («фальсифицирует») её. Однако если обратиться к истории естествознания, то можно увидеть, что реальная судьба эмпирических гипотез не так проста. Если гипотеза многократно раньше подтверждалась, давно и успешно использовалась в практике, то ее сторонники не спешат от нее отказаться при первой неудаче. Они подвергают сомнению эксперимент, если после всех перепроверок неприемлемый факт остаётся фактом, то старая гипотеза заменяется новой, которая в состоянии объяснить как все прежние, так н вновь обнаруженные явления. Новая гипотеза может отражать принципиально новую точку зрения новую парадигму) в данной научной области или же, что бывает чаще, представлять собой некоторую модификацию старой.

Остановимся на анализе примера, приведенного Д. Юмом. В результате обобщения фактов посредством индукции через простое перечисление было сформировано суждение: все лебеди - белы (1). В дальнейшем оказалось, что это обобщение является неверным: в Австралии были обнаружены черные лебеди. Таким образом, было опровергнуто суждение (1). Это, однако, не означало, что наша обобщающая деятельность, выразившаяся в формулирования суждения (1), была бесполезной. Обнаружение черных лебедей заставило к числу известных ранее шести видов лебедей, объединяемых в род Cygnus, добавить новый род и вид Chenopsis (Chenopsisatrata). Открытие черных лебедей, следовательно, привело в логическом смысле к расщеплению одного понятия на два; в биологическом смысле - вместо одного рода появилось два. Таким образом, вместо суждения (1) можно сфор­мулировать два: все лебеди рода Cygnus являются белыми, и все лебеди рода Chenopsis являются черными.

Обобщая изложенное выше, можно сказать, что опровержение противоречащими примерами общих утверждений, даже если они получены индукцией через простое перечисление, не означает их конкретизацию - внесение различий в тождественное.

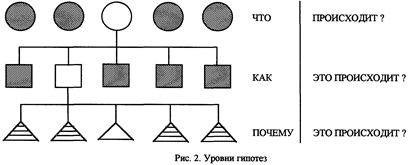
Б. Прежде чем перейти к рассмотрению элиминативной индукции, обсудим, в каких же случаях гипотеза кажется наиболее правдоподобной. Иногда, сравнивая две гипотезы, говорят, что одна из них лучше потому, что она может быть глубже объяснена. Условно можно выделить следующие уровни гипотез (рис. 2):

- ч т о происходит?

- к а к это происходит?

- п о ч е м у это происходит?

Можно было бы и дальше задавать вопросы: а это почему? а это как? и т. д. до бесконечности. Однако интересно отметить то людей, вышедших из возраста «почемучек», обычно удовлетворяет всего два-три уровня объяснения. Может быть, это связано с ограниченностью человеческой оперативной памяти (дальше человек забывает, с чего он начал), или с тем, что более отдаленные причины уже мало сказываются на специфике изучаемого явления, или с тем и другим, вместе взятыми. Таким образом, указание причины явления может сыграть решающую роль идя перевода гипотезы в разряд правдоподобных.

Приведем следующий пример. Классический образец абсурда обычно иллюстрируется высказыванием: «В огороде - бузина, а в Киеве - дядька». Попытаемся из этого высказывания сформулировать некоторую гипотезу о том, что всегда имеют место одновременно два события: 1) в огороде цветет бузина, 2) конкретный «дядька» находится в Киеве. Свяжем оба события такой информацией: «Дядька - житель Киева, пенсионер, все свое время проводит на даче, кроме того периода, когда цветет бузина. Почему? Потому что у него аллергия к цветам бузины». Теперь видно, что классический образец абсурда оказался вполне правдоподобной гипотезой.

Таким образом, мы вплотную подошли к элиминативной индукции, ибо, по словам Д. С. Мидия, понятие о причине есть корень всей теории индукции.

Еще эпикурейцы считали главной целью и основным содержанием индуктивного метода отыскивание причинно-следственных зависимостей. В этой связи они подчеркивали большое значение для правильного индуктивного метода не только сходства, но и различия между анализируемых примерами. В частности, они имели понятие об индуктивном методе единственного сходства. Более того эпикуреец Бромий считал, что доказательность индукции зависит не столько от числа положительных примеров, сколько от того, существен ли признак, по которому делается индукция.

Существенный вклад в развитие элиминативной индукции внесли Ф. Бэкон и Д. С. Милль. В 1620 г. в книге «Новый Органон» Ф. Бэкон фактически обосновал подход к индуктивным выводам как к процедурам обнаружения закономерностей (в отличие от понимания индукции лишь как перечислительной) и создал таблицы присутствия и отсутствия свойств, таблицы степеней присутствия свойств, которые можно рассматривать как первые попытки формализации фигур индуктивного рассуждения. Развитием идей Ф. Бэкона были, предложенные Д. С. Миллем, следующие методы (модусы) индуктивных выводов.

Метод сходства. Если два или более случая подлежащего исследованию явления имеют общим лишь одно обстоятельство, то это обстоятельство, в котором только и согласуются все эти случали, есть причина (или следствие) данного явления.

Метод различия. Если случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает, сходны во всех обстоятельствах, кроме одного, встречающегося лишь в первом случае, то это обстоятельство, в котором они только и разнятся, есть следствие, или причина, или необходимая часть причины.

Метод сопутствующих изменений. Всякое явление, изменяющееся определенным образом всякий раз, когда некоторым особенным образом изменяется другое явление, есть либо причина, либо следствие этого явления, либо соединено с ним какою-либо причинною связью.

Метод остатков. Если из явления вычесть ту его часть, которая, как известно из прежних индукций, есть следствие некоторых определенных предыдущих, то остаток данного явления должен быть следствием остальных предыдущих.

Соединенный метод сходства и различия. Если два или более случая возникновения явления имеют общим лишь одно обстоятельство и два или более случая невозникновения того же явления имеют общим только отсутствие того же самого обстоятельствам то это обстоятельство, в котором только и разнятся оба ряда случаев, есть или следствие или причина, или необходимая часть причины изучаемого явления.

«Главную задачу индукции, - писал Д.С.Милль, - составляет установление того, какие именно законы причинной связи существуют в природе, т. е. определение следствий каждой причины и причины каждого следствия. Указать, как решается эта задача, - вот главный предмет индуктивной логики».

В дальнейшем основное возражение всех представителей элиминативной индукции против энумеративной по существу сводится к критике методики выбора случаев. В энумеративной индукции случаи выбираются произвольным образом, лишь по признаку некоторого их сходства, дающего основание рассматривать их как случаи одного и того же класса, причем вопрос о существовании этого признака остается открытым и в конце концов решается post factum, в результате успеха или неуспеха самой индукции. Не возражая вообще против выбора случаев, в чем-то сходных, представители элиминативной индукции между тем настаивают на такой выборке, которая предполагала бы это сходство в условиях максимального разнообразия или варьируемое™ элементов исследуемого класса. Тогда то общее, что сохраняется в максимально отличных друг от друга проявлениях одного и того же случая, исчезает с исчезновением этого случая или изменяется с его изменением, только и может стать объектом индуктивного обобщения. При таком подходе в начале исследования, естественно, берется несколько .конкурирующих между собой гипотез, которые в процессе индуктивного анализа постепенно исключаются (элиминируются - отсюда название индукции - элиминативная) в пользу какой-либо одной гипотезы.

С. Теперь рассмотрим третий вид (индукции - индукцию как обратную дедукцию. Решающий вклад здесь внесли И. Ньютон, В. Уэвелл и особенно Ст. Джевонс. Исследуя соотношение индукции и дедукции. Ст. Джевонс писал: «В дедукции мы имеем дело с развитием выводов из закона. Индукция же есть совершенно обратный процесс. Здесь даются известные результаты и требуется открыть общий закон, из которого они вытекают». Вот почему индукцию как обратную дедукцию называют часто «объясняющей» индукцией.

И. Ньютон, В. Уэвелл и Ст. Джевонс трактуют индукцию прежде всего как метод открытия общих законов и принципов, объясняющих известные факты и менее общие законы и принципы. При этом все они сознавали неоднозначный (и в этом смысле не чисто логический) характер движения познающей мысли при индуктивном восхождении от фактов к объясняющим, их законам и принципам. Вместе с тем индуктивное восхождение не является с их точки зрения и чисто произвольным, полностью интуитивным, никак не регулируемым нормами логики процессом. Индуктивное восхождение является «правильным» тогда и только тогда, когда факты (основа, исходный пункт индуктивного восхождения) могут быть чисто логически (дедуктивно) выведены из предложенного для их объяснения закона или принципа.

В этой связи необходимо отметить работу Плоткина и описанный им метод индуктивного обобщения. Этот метод, хотя и не имел практического применения а реальных ЭС, тем не менее существенным образом повлиял на многие исследования в области автоматического порождения индуктивных гипотез.