Дедуктивный вывод на семантических сетях

Как мы говорили, в семантической сети вершины представляют собой понятийные объекты, а дуги – семантические отношения.

Семантические отношения классифицируются на:

а) структурные;

б) логические;

в) процедурные.

Пример: Между понятиями СТУДЕНТ КУРСА и ДИСЦИПЛИНА имеется структурная связь.

Между понятиями УСПЕВАЮЩИЙ и СТУДЕНТ имеется логическая связь: всякий индивидуум, принадлежащий понятию УСПЕВАЮЩИЙ, принадлежит и понятию СТУДЕНТ.

Более сложная логическая связь наблюдается между понятиями УСПЕВАЮЩИЙ, ОЦЕНКА, БАЛЛ и ДИСЦИПЛИНА: индивидуум является успевающим тогда и только тогда, когда его оценка по любой дисциплине не меньше 3 баллов.

Между понятиями СРЕДНЯЯ УСПЕВАЕМОСТЬ, ГРУППА и ДИСЦИПЛИНА имеется процедурная связь: средняя успеваемость студентов по данной дисциплине в группе вычисляется как среднее арифметическое оценок всех студентов из группы, полученных ими по данному предмету.

В системах, основанных на семантических сетях, используются структурные связи, а логические и процедурные связи применяются меньше. Слабое использование логических связей сильно ограничивает дедуктивные способности систем, поэтому в дальнейшем основное внимание будет уделено логическим связям.

Рассмотрим примеры высказываний и их соответствующие семантические сети.. Пусть дано выражение: «куб №2 находится всегда в том же месте, где куб №1». В форме дизъюнкта это выражение имеет вид: В(куб1,х)ÉВ(куб2,х).

Здесь В – предикат «находится в месте», а х представляет собой любой индивидуум (связан квантором общности).

Утверждение «куб №1 находится в месте а» будем записывать как

ИÉВ(куб1,а) или в сокращенной форме

ÉВ(куб1,а) и считать консеквентом.

Выражение «куб №1 не находится в месте а» будет иметь вид:

В(куб1,а)É Л или в сокращенной записи

В(куб1,а)É и оно считается антецедентом.

Если в выражениях имеются кванторы $, то переменные, связанные этими кванторами, заменяются скулемовскими функциями, а оставшиеся кванторы общности удаляются, считая, что все переменные, ими связанные, являются универсально квантифицированными. Для каждой совокупности дизъюнктов можно построить эквивалентную ей семантическую сеть. Семантические сети должны быть организованы таким образом, чтобы извлечение, вывод и анализ информации происходил по возможности быстрее и эффективнее. С этой целью над семантическими сетями введем операцию типа раскраски семантических сетей. В этом случае семантические сети представляются в виде раскрашенных ориентированных графов. Представление в раскрашенном виде семантических сетей уменьшает перебор при поиске информации, а также помогает во время вывода новых утверждений, что повышает эффективность работы системы. Примем следующие правила раскраски:

а) цветом Ц₁ (непрерывная линия) будем раскрашивать антецеденты;

б) цветом Ц₂ (пунктирная линия) – консеквенты.

Поясним сказанное примером. Пусть имеем следующий набор высказываний:

1. Если куб №1 находится на месте а, то куб №2 тоже находится в том же месте.

2. Если куб №1 находится на месте а, то куб №3 находится в месте b.

3. Куб №1 находится в месте а.

В дизъюнктивной форме:

1. В(куб1,а) ÉВ(куб2,а) – P₁, P₂, P₃ – пропозиц. символы

2. В(куб1,а)ÉВ(куб3,b) – P₄, P₅, P₆ – пропозиц. символы

3. ÉВ(куб1,а) – P₇ – пропозиц. символ

Соответствующая раскрашенная семантическая сеть представлена на рис.1. В сети буквой Р₁ обозначена пропозициональная вершина, соответствующая первому высказыванию в целом, пропозициональные вершины P₂ и P₃ обозначают соответственно антецедент В(куб1,а) и консеквент В(куб2,а) то и другое в целом. Далее расписываются антецедент и консеквент. Антецедент состоит из термов «куб1», «а» и предиката В – « находится в месте», а консеквент – из термов «куб2», «а» и того же предиката В. Аналогично расписываются остальные высказывания.

Допустим, необходимо найти в сети утверждение ÉВ(куб1,а). Сначала находим все пропозициональные символы, связанные с вершинами «В», «куб1» и «а». Это – P₂, P₅, P₇, т.к. P₂ и P₅ являются антецедентами, то они исключаются, а вершине P₇ соответствует третье утверждение. Аналогично находится любое другое утверждение.

Такой подход использует локальное возбуждение того или иного участка сети, что значительно уменьшает время поиска нужного утверждения. Таким образом, преимущество данного подхода заключается в следующем:

1) дается эффективная индексация информации с помощью раскрашенных графов, что позволяет обрабатывать сети большой размерности;

2) эффективно удаляется из сети информация, не относящаяся к данному вопросу.

В дальнейшем для простоты будем изображать семантическую сеть, состоящую из дизъюнктивных вершин, т.е. вершин, которым соответствуют исходные дизъюнкты, предикатных вершин и дуг, помеченных двумя цветами. Тогда, после упрощений приведенная выше семантическая сеть будет иметь вид:

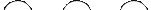где g₁, g₂, g₃ – исходные дизъюнкты, В – предикат.

Такие упрощенные сети называются L-сетями, которые задаются четверкой:

L=<G,P,F₁,F₂> (1)

P – множество предикатных вершин

G – множество дизъюнктных вершин

F₁, F₂ – отображение G в Р, представляемое множеством дуг, помеченных соответственно цветами Ц₁ и Ц₂.

L-сети введены нами только для удобства иллюстрации процедур дедуктивного вывода. Семантические сети, являясь формализмом представления знаний в СИИ, обладают, таким образом, следующими особенностями:

1) в семантической сети представлены такие виды объектов как понятия, события, ситуации, а также специализированные методы выводы. При этом следует учесть, что увеличение номенклатуры объектов снижает однородность сети и приводит к необходимости увеличения количества методов вывода;

2) многомерность семантических сетей позволяет представить в них многочисленные семантические отношения, связывающие отдельные понятия, понятия и события в предложениях, а также предложения в текстах. Кроме того, в семантической может быть отражена семантическая иерархия специализированных методов вывода, определяющая их взаимоподчиненность;

3) формализация, как структурное представление семантических знаний, позволяет наложить на эти знания некоторую суперсемантику, отражающую относительную «силу» семантических отношений, что способствует повышению эффективности вывода в семантических сетях;

4) на каждой стадии решения задачи можно четко полное знание системы (полная семантическая сеть) и текущее знание – возбужденный участок семантической сети, в котором производятся некоторые операции (процесс «понимания», вывода и т.д.).

Необходимо учесть, что семантические представления часто проигрывают в представлении чисто структурных отношений, легко реализуемых в исчислении предикатов или процедурном представлении. Поэтому ряд современных исследований в области представления знаний идет по пути вложения в семантическое представление некоторых фрагментов процедурных или декларативных представлений с целью объединения их преимуществ в новом, комбинированном представлении. В настоящее время разработаны различные виды дедуктивных выводов на семантических сетях как резолютивные, так и нерезолютивные. Рассмотрим резолютивный метод вывода, известный как алгоритм семантической унификации.

Алгоритм семантической унификации двух дизъюнктов такой же, как тот, который мы рассмотрели с вами в прошлой лекции. Этот алгоритм работает при поиске резольвенты двух дизъюнктов.

Описание алгоритма:

1) если в сети есть вершина свободная от мультидуг, то на следующий шаг, иначе на шаг 8;

2) выделяем предикатную вершину Р, которая свободна от мультидуг;

3) вычисляем A={F₁(P)} – множество вершин с дугами цвета Ц₁, входящих в вершину Р;

4) вычисляем В={F₂(P)} – множество вершин с дугами цвета Ц₂, входящих в вершину Р;

5) F=AÈB

6) резольвируем дизъюнкты из множества F по предикату Р. Если получили , то остановка;

7) в семантическую сеть добавляются все дизъюнкты, сгенерированные в шаге 6, и из семантической сети удаляются все дизъюнкты из множества F, затем переход на шаг 1;

8) применяем оператор расщепления, пока не получим вершину, свободную от мультидуг и переходим на шаг 2.

Данный алгоритм основан на преобразовании семантических сетей. Теперь рассмотрим алгоритм, в котором в процессе вывода семантическая сеть не изменяется.

Основная идея алгоритма состоит в следующем: для данной предикатной вершины Р выбирается любая контрарная пара литер, которая затем резольвируется. Если вершина содержит другие контрарные пары, то они рассматриваются, как альтернативные, и их выбор происходит только после неудачи с унификацией текущей контрарной пары.

Если в вершину входят дуги только одного цвета (так называемые «чистые» дизъюнкты), то они не влияют на процесс вывода пустой сети и удаляются из рассмотрения. Процесс продолжается до тех пор, пока не будет выведена пустая сеть. Приведем более детальную интерпретацию метода.

Обозначим через CLIST – рабочий список, а ALIST – список альтернатив.

1) CLIST = 0; ALIST = 0;

2) A = {F₁(g) È F₂(g)};

3) множество А модифицируется таким образом, чтобы каждый элемент имел вид (1);

4) CLIST = A

5) берется первый элемент из CLIST, имеющий вид (P,g,I), где Р – предикатный символ, g – имя дизъюнкта, а I=1, если дуга (g,P) цвета Ц₁ и I=2, если дуга (g,P) цвета Ц₂. Из CLIST исключается первый элемент.

6) Если I=1, то G={F₂^–1(P)}\g;
Если I=2, то G={F₁^–1(P)}\g, где F₁^–1 и F₂^–1 – отображения, обратные F₁ и F₂.

7) для всех g’ÎG повторяются шаги 8–15 до тех пор, пока не будет исчерпан список G.

8) B={F₁(g’) È F₂(g’)}

9) модифицируется В в соответствии с (1);

10) берется первый элемент (P’,g’,I’) из списка В и он исключается из этого списка, причем имена Р и Р’ совпадают, а I’=1, если I=2 и I’=2, если I=1. Если таких элементов нет для "g’ÎG, то переход на шаг 17.

11) находим НОУ s для Р и Р’

12) B=B È CLIST

13) B=Bs

14) если В=Æ, то процедура завершилась успешно, в противном случае переход на шаг 15.

15) первым элементом ALIST становится подсписок В.

16) выбирается первый элемент из ALIST и он удаляется из СLIST, переход на шаг 5.

17) если ALIST=Æ, то процедура завершилась неудачно, в противном случае в СLIST заносится первый элемент ALIST, и этот элемент удаляется из ALIST.

18) переход к шагу 5.

Пример:

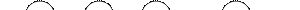
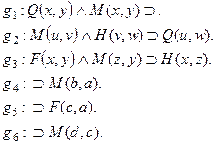
1. CLIST = Æ, ALIST = Æ

2. A = {F₁ (g₁) È F₂ (g₁)} = {M, Q}

3. A = {(M(y, a), g₁ , 1), (Q(x, y), g₁ , 1)}

4. CLIST = A

5–15. G = {g₄ , g₆}

b = {F₁ (g₄) È F₂ (g4)} = {M}

B = { (M (b,a), g₄ , 2)}

s = {b / y}

В дальнейшем для краткости будем записывать только изменения CLIST и ALIST.

16. CLIST = {(Q(x, b), g₁ , 1)}

s = {x / u, b / w}

CLIST = {(M(x,v), g₂ , 1), (H(v, b), g₂ , 1)}

s = (b / x, a / v}

CLIST = {(H(a, b), g₂ , 1)}

s = {a / x, b / z}

ALIST = {{(H(c, b), g₂ , 1)}}

CLIST = {(M(b, y), g₃ , 1), (F(a, y), g₃, 1)}

s = {a / y}

CLIST = {(F(a, a), g₃ , 1)}.

Тупик и переход к пункту 17.

17. CLIST = {(H(с, b), g₂ , 1)} – первый элемент ALIST

ALIST = Æ – исключаем первый элемент из ALIST

s = {c / x, b / z}

CLIST = {(M(b, y), g₃ , 1), (F(c, y), g₃, 1)}

s = {a / y}

CLIST = {(F(c, a), g₃, 1)}

s = Æ

Процедура завершилась успешно. Этот алгоритм позволяет обрабатывать сети большой размерности и эффективно находить решение.