Семантическая резолюция

Обратимся теперь к стратегии семантической резолюции, предло­женной Слэйглом. Стратегия на основе семантической резолюции так­же использует упорядочение литер, как и OL -резолюция. Кроме того, эта стратегия основывается на разделении всего множества исходных и порождаемых дизъюнктов на два непересекающихся класса, назовем их Т и F. Такое разбиение возможно, если задать некоторую интерпре­тацию I для формул исходного множества. В интерпретации I часть дизъюнктов окажется истинной, а часть ложной. Множество истинных дизъюнктов в интерпретации I - это по определению множество Т; мно­жество ложных дизъюнктов в интерпретации I - это по определению есть множество F.

При построении вывода требуется выполнение двух условий:

1) резольвента строится для дизъюнктов С₁ и С₂ таких, что С₁ Î T, а C₂ Î F

2) отсекаемая литера в дизъюнкте С₂ должна быть самой правой литерой.

Пусть E₁, E₂, ..., E_q некоторое множество дизъюнктов, принадлежа­щих F, а N - дизъюнкт из Т.

Тогда множество {E₁, E₂, ..., E_q, N} называется клашем, если вы­полняется следующее условие:

(i) R₁ = N;

(ii) i < 1, R_i+1 есть резольвента R_i-1 и E_i-1­; отсекаемая литера - старшая в E_i (самая правая);

(iii) R_q+1 Î F.

R_q+1 называется резольвентой данного клаша.

Пример. Пусть

C₁ = R Ú 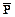Ú ,

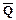C₂ = P Ú R,

C₃ = Q Ú R,

C₄ = ,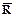

P > Q > R >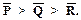

Пусть в интерпретации I R - ложен, Р - ложен, Q - ложен. Тогда клашами являются множества

K₁ = {С₃, C₄},

K₂ = {C₂, C₄}.

Вывод на основе семантической резолюции строится так, что каж­дый дизъюнкт либо принадлежит исходному множеству дизъюнктов, либо является резольвентой некоторого клаша.

Так резольвентой С₅ клаша К₁ является Q; резольвентой С₆ клаша К₂ является Р.

Резольвентой С₅ и С₁ является дизъюнкт C₇ = R Ú .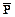

Резольвентой С₇ и С₆ является дизъюнкт С₈ = R.

Резольвентой дизъюнктов С₈ и С₄ является .

Резолюция в PL

Применению OL-вывода в PL предшествует подготовительный этап, предложенный Девисом и Патнемом. Он включает в себя 3 стадии:

1) преобразование формулы в ПНФ;

2) преобразование матрицы в КНФ;

3) преобразование формулы в ССФ.

С реализацией второй стадии вы хорошо знакомы, поэтому рассмотрим 1-ю и 3-ю стадии.

В L имеются две нормальные формы: ДНФ и КНФ, в PL роль нормальной формы играет ПНФ – предваренная нормальная форма.

Определение: Говорят, что формула F в PL находится в ПНФ тогда и только тогда, когда формула F имеет вид: (Q₁x₁)…(Q_nx_n)(M), где (Q_ix_i) (i=1,…,n) есть либо ("x_i), либо ($x_i) и М есть формула, не содержащая кванторов.

(Q₁x₁)…(Q_nx_n) называется префиксом формулы F, М – матрицей формулы F.

Для преобразования формулы F в ПНФ используются законы эквивалентных преобразований, называемых законами принесения кванторов через Ù и Ú:

(1а) (Qx)F(x)ÚG=(Qx)(F(x)ÚG)

(1б) (Qx)F(x)ÙG=(Qx)(F(x)ÙG)

(2а) Ø(("x)F(x))=($x)(ØF(x))

(2б) Ø(($x)F(x))=("x)(ØF(x))

(3а) ("x)F(x)Ù("x)M(x)=(" x)( F(x)ÙM(x))

(3б) ($x)F(x)Ù($x)M(x)=($ x)( F(x)ÙM(x))

Однако " и $ нельзя проносить через Ú и Ù соответственно. В подобных случаях нужно поступать специальным образом. Т.к. каждая связанная переменная в формуле может рассматриваться лишь как место для подстановки какой угодно переменной, то каждую связанную переменную х можно переименовать в z и формула ("x)M(x) перейдет в ("z)M(z), т.е. ("x)M(x)= ("z)M(z). Предположим, что мы выбираем переменную z, которая не встречается в F(x). Тогда ("x)F(x)Ú ("x)M(x)= ("x)F(x)Ú ("z)M(z) путем замены всех х, входящих в ("x)M(x) на z, тогда согласно (1а):

(4а) ("x)F(x)Ú ("x)M(x)= ("x)("z)(F(x)Ú M(z))

(4б) ($x)F(x)Ú ($x)M(x)= ($x)($z)(F(x)Ú M(z)).

Преобразование формул в ПНФ:

1) используем законы, чтобы исключить логические связки ~ и É

(5) F~G=(FÉG)Ù(GÉF)

(6) FÉG=ØFÚG

2) используем законы, чтобы пронести знак отрицания внутрь формулы

(7) Ø(ØF)=F

(8) Ø(FÚG)=ØFÙØG

(9) Ø(FÙG)=ØFÚØG

(10) Ø(("x)F(x))=($x)(ØF(x))

(11) Ø(($x)F(x))=("x)(ØF(x))

3) переименовываем связанные переменные, если это необходимо

4) используем законы (1а–4б), чтобы вынести кванторы в самое начало формулы для получения формулы, находящейся в ПНФ.

Пример 1: приведем формулу ("x)P(x)É($x)Q(x).

("x)P(x)É($x)Q(x)=

=Ø(("x)P(x))Ú($x)Q(x)= по (6)

=($x)(ØP(x))Ú($x)Q(x)= по (2а)

=($x)(ØP(x)ÚQ(x)) по (3б)

где ($x) – префикс, а (ØP(x)ÚQ(x)) – матрица.

Пример 2: получить ПНФ для формулы:

("x)("y)(($z)P(x,z)ÙP(y,z))É ($u)Q(x,y,u))=

= ("x)("y)(Ø(($z)P(x,z)ÙP(y,z)))Ú ($u)Q(x,y,u))= по (6)

= ("x)("y)("z)(ØP(x,z)ÙØP(y,z))Ú ($u)Q(x,y,u))= по (2б) и (9)

= ("x)("y)("z)($u)(ØP(x,z)ÙØP(y,z))Ú Q(x,y,u)) по (1а)

где ("x)("y)("z)($u) – префикс, а (ØP(x,z)ÙØP(y,z))Ú Q(x,y,u)) – матрица.

Рассмотрим вопрос преобразования формулы F в скулемовскую стандартную форму (ССФ).

Для этого мы должны, сохраняя противоречивость формулы, элиминировать в ней кванторы существования путем использования скулемовских функций.

Условимся, что формула F находится в ПНФ:

(Q₁x₁)…(Q_nx_n)M, где М в свою очередь находится в КНФ, тогда:

1) выберем самый левый квантор существования Q_r в префиксе (Q₁x₁)…(Q_nx_n) (1£r£n);

2) если никакой " не стоит в префиксе левее Q_r, то выберем новую константу С, отличную от других констант, входящих в М, заменим все х_r, встречающиеся в М, на С и вычеркнем (Q_rx_r) из префикса;

3) Если Q_s1,…,Q_sm – список всех ", стоящих левее Q_r, (1£S₁<S₂<…<S_m<r), то выберем новый m-местный функциональный символ f, отличный от других функциональных символов, заменим все x_r в M на f(x_s1,…,x_sm) и вычеркнем (Q_r,x_r) из префикса;

4) Весь этот процесс применим для всех $ в префиксе, двигаясь слева направо (следует отметить, что порядок выбора $ из префикса несущественен).

Последняя из полученных формул и есть ССФ формулы F (или просто стандартная форма формулы F). Константы и функции, используемые для замены переменных $, называются скулемовскими функциями.

Пример 1: получить стандартную форму формулы ($x)("y)("z)($u)("v)($w) P(x,y,z,u,v,w).

В этой формуле левее ($x) нет ни одного ", значит заменяем х на а.

($u) находится ("y)("z), значит заменяем u на f(y,z)

($w) находится ("y)("z)("v), значит заменяем w на g(y,z,v).

Тогда ("y)("z)("v)P(a,y,z,f(y,z),v,g(y,z,v)) – стандартная форма.

При использовании процедур опровержения не происходит потери общности, поэтому при доказательстве кванторы общности можно опустить.

Рассмотрим теперь непосредственнометод резолюций,применяемый в PL при построении OL-вывода.

Как и в L здесь существенным является нахождение в дизъюнкте литеры, которая контрарна литере в другом дизъюнкте. Рассмотрим дизъюнкты: С₁: P(x)ÚQ(x) и C₂: ØP(f(x))ÚR(x).

С первого взгляда в С₁ нет литеры, контрарной какой-либо литере в С₂, однако если подставить f(0) вместо x в С₁ и a вместо x в C₂, то получим: С₁’: P(f(a))ÚQ(f(a)) и C₂’: ØP(f(a))ÚR(a).

C₁’ и C₂’ называются основными примерами С₁ и С₂ соответственно, а P(f(a)) и ØP(f(a)) контрарны друг другу. Следовательно, из C₁’ и C₂’ можно получить резольвенту:

C₃’: Q(f(a))ÚR(a).

В общем случае, подставив f(x) вместо x в C₁, получим: C₁^*: P(f(x))ÚQ(f(x)). Снова С₁^* есть пример С₁. Литера P(f(x)) из С₁^* контрарна литере ØP(f(x)), тогда резольвента С₁^* и С₂:

С₃: Q(f(x))ÚR(x).

При этом С₃’ является примером С₃. Кроме того, дизъюнкт С₃ является наибольшим общим дизъюнктом в том смысле, что все другие дизъюнкты, порожденные подобным образом, есть приме

С₃ будем называть резольвентой С₁ и С₂. Таким образом, получение резольвенты из двух дизъюнктов в PL связано с подстановкой.

Определение: Подстановка – это конечное множество вида {t₁/v₁,…,t_n/v_n}, где каждая v_i – переменная, а t_i – терм, отличный от v_i, при этом все v_i различны. Если t₁,…,t_n – основные термы, то подстановка называется основной. Подстановка, которая не содержит элементов, называется пустой и обозначается e. Будем использовать греческие буквы для обозначения подстановки.

Определение: Пусть q ={t₁/v₁,…,t_n/v_n} – подстановка и Е – выражение. Тогда Еq – выражение, полученное из Е заменой одновременно всех вхождений переменной v_i (1£i£n) в Е на t_i. Еq называют примером Е.

Определение: Пусть q ={t₁/x₁,…,t_n/x_n} и l={u₁/y₁,…,u_m/y_m} – две подстановки. Тогда композиция q·l есть подстановка, которая получается из множества {t₁/x₁,…,t_n/x_n,u₁/y₁,…,u_m/y_m} вычеркиванием всех элементов t_jl/x_j, для которых t_jl = x_j, и всех элементов u_i/y_i, таких что y_iÎ{x₁,…,x_n}.

Пример: q ={t₁/x₁, t₂/x₂}={f(y)/x, z/y}

l ={u₁/y₁, u₂/y₂, u₃/y₃}={a/x, b/y, y/z}, тогда

q·l={t₁/x₁, t₂/x₂, u₁/y₁, u₂/y₂, u₃/y₃}={ f(y)/x, z/y, a/x, b/y, y/z}

Так как t₂l=x₂, а именно z/y, то этот элемент вычеркивается из множества y₁ и y₂Î {x₁, x₂, x₃}, т.е. a/x и b/y должны быть тоже вычеркнуты. Таким образом, получаем:q·l={f(b)/x, y/z}.

Композиция подстановок ассоциативна, а пустая подстановка e есть одновременно и левое и правое тождество, т.е. (q·l)·m=q·(l·m) и e·q=q·e для всех m,q, l.

В процедуре доказательства по методу резолюций зачистую приходится отождествлять контрарные пары литер. Для этого необходимо унифицировать (склеивать) два и более выражение, т.е. мы должны найти подстановку, которая может сделать несколько выражений тождественными.

Рассмотрим унификацию выражений.

Определение: Подстановка q называется унификатором для множества {E₁,…,E_k} Û E₁q =E₂q =…=E_kq.

Говорят, что множество {E₁,…,E_k} унифицируемо, если для него существует унификатор.

Определение: Унификатор s для множества выражений {E₁,…,E_n} будет наиболее общим унификатором (НОУ) Û для каждого унификатора q для этого множества существует такая подстановка l, что q = s·l.

Определение: Множество рассогласований D непустого множества выражений W получается выявлением первой (слева) позиции аргумента, на которой не для всех выражений из W стоит один и тот же символ.

Алгоритм унификации

1. Множество k = 0, W_k = W, s_k =e.

2. Если W_k – единичный дизъюнкт, то остановка, s_k – НОУ для W, иначе найдем множество рассогласований D_k для W_k.

3. Если существуют такие элементы v_k и t_k в D_k, что v_k – переменная, не входящая в t_k,то перейдем к шагу 4. В противном случае остановка: W не унифицировано.

4. Пусть s_k+1=s_k·{t_k/v_k} и W_k+1=W_k·{t_k/v_k}

5. Присвоить значение k+1 и перейти к шагу 2.

Пример: Найти НОУ для W={P(a,x,f(g(y))),P(z,f(z),f(u))}.

1. v₀=e и w₀=w

2. D₀={a,z}. Переменной в этом множестве является z, значит v₀=z, а t₀=a

3. v₁=v₀·{t₀/v₀} = e·{a/z}={a/z},
w₁=w₀·{t₀/v₀}={P(a, x, f(g(y))), P(z, f(z), f(u))} · {a/z} = {P(a, x, f(g(y))), P(a, f(a), f(u))}

4. w₁ – не единичный элемент. D₁={x,f(a)}

5. Из D₁ следует v₁=x, t₁=f(a)

v₂=v₁·{t₁/v₁} = {a/z}·{f(u)/x}={a/z,f(u)/x},
w₂=w₁·{t₁/v₁}={P(a, x, f(g(y))), P(a, f(a), f(u))} · {f(a)/x} = {P(a, f(a), f(g(y))), P(a, f(a), f(u))}

6. Для w₂: D₂={g(y),u}, v₂=u, t₂=g(y)

7. v₃=v₂·{t₂/v₂} = {a/z, f(u)/x}·{g(y)/u}={a/z, f(u)/x, g(y)/u}
w₃=w₂·{t₂/v₂}={P(a, f(a), f(g(y))), P(a, f(a), f(u))} · {g(y)/u} = {P(a, f(a), f(g(y))), P(a, f(a), f(g(y)))}={P(a, f(a), f(g(y)))}

8. s₃= {a/z, f(a)/x, g(y)/u} – НОУ для W.

Пример:

S={M(a, S(c), S(b)), P(a), M(x, x, S(x)), ØM(x, y, z) Ú M(y, z, x), ØM(x, y, z) Ú D(x, z), ØD(a, b), ØP(w) Ú ØM(y,z,z) Ú ØD(w,z) Ú D(w,x) Ú D(w,y)}

Введем дополнительные определения.

1. Дизъюнкт есть дизъюнкция литер. Иногда когда это удобно, мы будем рассматривать множество литер как синоним дизъюнкта. Например, P Ú Q Ú R = {P, Q, R}.

2. Дизъюнкт, содержащий r литер, называется r- литерным дизъюнктом;

3. Однолитерный дизъюнкт называется единичным дизъюнктом;

4. Когда дизъюнкт не содержит никаких литер, мы называем его пустым дизъюнктом.

Дизъюнкты ØP(x, f(x)) Ú R(x,f(x),g(x)) и Q(x,g(x)) Ú R(x, f(x), g(x)) суть дизъюнкты. Считаем, что множество дизъюнктов S есть конъюнкция всех дизъюнктов из S, где каждая переменная в S считается управляемой квантором всеобщности. Благодаря этому соглашению стандартная форма может быть просто представлена множеством дизъюнктов. Например, стандартная форма в примере 2 может быть представлена множеством

S = {ØP(x, f(x)) Ú R(x, f(x), g(x)), Q(x, g(x)) Ú R(x, f(x), g(x))}.

Мы можем элиминировать кванторы существования, сохраняя противоречивость формулы. Формула F противоречива (не выполнена) Û не существует интерпретация, которая удовлетворяет F. Покажем это в следующей теореме.

Теорема 1. Пусть S – множество дизъюнктов, которые представляют стандартную форму формулы F. Тогда F противоречива в том и только в том случае, когда S противоречива.

Доказательство. Без потери общности можно положить, что F находится в предваренной нормальной форме, т.е. F = (Q₁x₁) … … (Q_nx_n) M [x₁, …, x_n]. (Мы используем M [x₁, …, …, x_n], чтобы указать, что матрица М содержит переменные x₁, …, x_n). Пусть Q_r – первый квантор существования. Пусть F₁ = ("x₁) … ("x_r-1) (Q_r+1x_r+1) … (Q_nx_n) M [x₁, …, x_{r-1, f}(x₁, …, x_r-1), x_r+1, …, x_n], где f – скулемовская функция, соответствующая x_r, 1£ r £ n. Мы хотим показать, что F противоречива тогда и только тогда, когда F₁ противоречива.

1. Предположим, что F противоречива, а F₁ непротиворечива, если F₁ непротиворечива, то существует такая интерпретация I, что F₁ истинна в I. Это означает, что для всех x₁, …, x_r-1 существует по крайней мере один элемент , для которого формула (Q_r+1x_r+1) … (Q_nx_n) M[x₁, …, …, x_r-1 , f(x₁, …, x_r-1), x_r+1 , …, x_n] истинна в I. И этим элементом является f (x₁, …, x_r-1). Таким образом, F истинна в I, что противоречит предположению, что F ппротиворечива. Следовательно, F₁ должна быть противоречива.

2. Предположим, что F₁ противоречива, а F непротиворечива. Если F непротиворечива, то существует такая интерпретация I на области D, что F истинна в I, т.е. для всех x₁, …, x_r-1 существует такой элемент х_r, что (Q_r+1x_r+1) … (Q_nx_n) M[x₁, …, …, x_r-1, x_r, x_r+1, …, x_n] истинна в I.

Расширим интерпретацию I, включая функцию f, которая отображает (x₁ , …, …, x_r-1) на x_r для всех x₁, …, …, x_r-1 в D, т.е. f (x₁ , …, …, x_r-1) = x_r. Пусть это расширение I обозначается I'. Ясно, что для всех x₁ , …, …, x_r-1 (Q_r+1x_r+1) … (Q_nx_n) M[x₁, …, …, x_r-1 , f( x₁ , …, …, x_r-1) x_r+1, …, x_n] истинна в I', т.е. F₁ истинна в I', что противоречит предположению, что F₁ противоречива. Следовательно, F должна быть противоречивой. Мы разобрали случай, когда формула имеет один $. Предположим теперь, что в F имеется m кванторов существования. Пусть F₀ = F. Пусть F_k получается из F_{k -1} заменой первого квантора существования в F_k--1 скулемовской функцией, k = 1, …, m. Следовательно, мы заключаем, что F противоречива тогда и только тогда, когда S противоречива, что и требовалось доказать.

Пусть S- стандартная форма формулы F. Если F противоречива, то по теореме 1 F = S. Если F непротиворечива, заметим, что, вообще говоря, F не эквивалентна S. Например, пусть F = ($x) P(x) и S = P(a). Ясно, что S есть следующая интерпретация:

Область: D = {1, 2}.

Значения для а:

___а___

1

Значения для Р:

_________Р______

P(1) P(2)

Л И

Тогда ясно, что F истинна в I, но S ложна в I. Таким образом, F ¹ S.

Отметим, что формула может быть иметь более чем одну стандартную форму. Ради простоты, когда мы преобразуем формулу F в стандартную форму S, мы будем заменять кванторы существования скулемовскими функциями настолько простыми, насколько возможно. Дальше, если мы имеем F = F₁ Ù … Ù F_n, мы можем отдельно получить множество дизъюнктов S_i, i = 1, …, n. Затем пусть S =S₁U …U S_n. С помощью рассуждений, подобных тем, которые даны в доказательстве теоремы 1, нетрудно увидеть, что F противоречива тогда и только тогда, когда S противоречива.

Пример 3. В этом примере покажем, как выразить следующую теорему в стандартной форме.

Если х*х = е для всех х в группе G, где * есть бинарный оператор и е есть единица группы G, то G коммутативна.

Сначала формализуем эту теорему вместе с некоторыми основными аксиомами теории групп и затем представим отрицание этой теоремы множеством дизъюнктов.

Известно, что группаG удовлетворяет следующим четырем аксиомам:

A₁: x, y Î G влечет x*y ÎG (свойство замкнутости);

A₂: x, y, z Î G влечет x*(y*z) = (x*y)*z (свойство ассоциативности);

A₃: x*e = e*x=x для всех x Î G (свойство существования единичного элемента);

A₄: для каждого элемента xÎG существует элемент x^-1ÎG такой, что x*x^-1 = x^-1*x = e (свойство существования обратного элемента).

Пусть P(x, y, z) обозначает x*y = z и i(x) обозначает x^-1. Тогда вышестоящие аксиомы примут вид:

A'₁: ("x) ("y) ($z) P(x, y, z);

A'₂: ("x) ("y) ("z) ("u) ("v) ("w) (P (x, y, u) Ù P(y, z, v) Ù P(u, z, w) ®P(x, v, w)) Ù("x) ("y) ("z) ("u) ("v) ("w) (P (x, y, u) Ù P(y, z, v) Ù P(x, v, w)®P(u, z, w));

A'₃: ("x) P (x, e, x) Ù ("x) P (e, x, x);

A^'₄: ("x) P (x, i (x), e) Ù("x) P (i(x), x, e).

Заключение теоремы такое:

B: Если х*х = е для всех х ÎG, то G коммутативна, т.е. u*v = v*u для всех u, v ÎG.

В может быть представлено формулой

B': ("x) P(x, x, e) ®(("u) ("v) ("w) (P(u, v, w)®P(v, u, w))).

3. Теперь вся формула представляется формулой F = A'₁ Ù …Ù A'₄®B'. Таким образом, ØF = A'₁ Ù A'₂ Ù A'₃ Ù A'₄ Ù ØB'. Чтобы получить множество дизъюнктов S для ØF, сперва получим множество дизъюнктов S_i для каждой аксиомы A’_i = 1, 2, 3, 4, следующим образом:

S’₁: {P (x, y, f(x, y))};

S’₂: {ØP(x, y, u) Ú ØP(y, z, v) Ú ØP(u, z, w) Ú P(x, v, w),

ØP(x, y, u) Ú Ø P(y, z, v) Ú ØP(x, v, w) Ú P(u, z, w)};

S₃: {P(x, e, x), P(e, x, x)};

S₄: {P(x, i(x), e), P(i(x), x, e)}.

Так как

ØB’ = Ø (("x) P(x, x, e) ® (("u) ("v) ("w) (P(u, v, w) ® P(v, u, w))))

= Ø (Ø("x) P(x, x, e) Ú (("u) ("v) ("w) (ØP(u, v, w) Ú P(v, u, w))))

= ("x) P(x, x, e) Ù Ø (("u) ("v) ("w) (ØP(u, v, w) Ú P(v, u, w)))

= ("x) P(x, x, e) Ù (($u) ($v) ($w) (P(u, v, w) Ù Ø P(v, u, w))).

то множество дизъюнктов для Ø B’ дается ниже.

T: {P(x, x, e), P(a, b, c), Ø P(b, a, c)}.

Таким образом, множество S = S₁ È S₂ È S₃ È S₄ È T есть множество, состоящее из следующих дизъюнктов:

(1) P(x, y, F(x, y)),

(2) Ø P(x, y, u) Ú Ø P(y, z, v) Ú ØP(u, z, w) Ú P(x, v, w),

(3) Ø P(x, y, u) Ú Ø P(y, z, v) Ú Ø P(x, v, w) Ú P(u, z, w),

(4) P(x, e, x),

(5) P(e, x, x),

(6) P(x, i(x), e),

(7) P(i(x), x, e),

(8) P(x, x, e),

(9) P(a, b, c),

(10) Ø P(b, a, c).

Пример 3 показывает, как получить множество дизъюнктов S для формулы Ø F. Из теоремы 1 известно, что F общезначима тогда и только тогда, когда S противоречива. Как говорилось в начале этого параграфа, для доказательства теоремы будем использовать процедуру опровержения. Таким образом, с этого места мы будем предполагать, что на входе процедуры опровержения стоит всегда множество дизъюнктов (такое как множество S, полученное в приведенном выше примере). Дальше мы будем использовать для множества дизъюнктов термины «невыполнимо» («выполнимо») вместо «противоречиво» («непротиворечиво»).