Резолюция в логике высказываний

Пусть А,В,С...- атомарные формулы логики высказываний. Фор­мулу вида (AÚBÚ...ÚD), где А, В,…, D- атомарные формулы, назовем дизъюнктом. Говорят, что два дизъюнкта С₁ и С₂ содержат контрарную пару литер X и 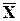, если они имеют следующее представление:

C₁ = RÚ...ÚX,

C₂ = QÚ...Ú .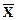

Пусть, например С₁ = А Ú X и С₂ = В Ú .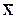

Тогда дизъюнкт (АÚВ)является резолюцией дизъюнктов С₁ и С₂.

Лемма. Пусть С₁ и С₂ - два дизъюнкта и I - атомарная формула. Если IÎC₁ и 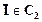, то дизъюнкт (С₁\{I}) 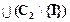является логичес­ким следствием дизъюнктов С₁ и С₂.

Доказательство. Пусть С_R - резольвента дизъюнктов С₁ и С₂.

Лемма утверждает, чтоC₁, C₂ ^|¾ C_R, что равносильно тождественной истинности формулыC₁ÙC₂ ® C_R.

Последняя ложна, если С₁ Ù С₂ истинно и С_R ложно.

Пусть С₁ = С_R Ú I и C₂ = С_R Ú .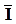

Имеем C₁ Ù C₂ = (C_R Ú I) Ù (C_R Ú 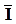) = C_R.

Следовательно, в силу преобразований логики высказываний С₁ Ù C₂ эквивалентна С_R, а это значит что С₁ÙC₂ ®C_R тождественно истинная формула.

На основании метода резолюций устанавливается невыполнимость некоторого множества дизъюнктов. Пусть требуется доказать, что фор­мула j выводима из формул e₁, e₂, ..., e_n, т.е. установить, что формула

e₁ Ù e₂ Ù...Ù e_n ® j (7.2)

тождественно истинна.

Это эквивалентно доказательству того, что формула

e₁ Ù e₂ Ù...Ù e_n Ù 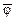(7.3)

является тождественно ложной.

Обозначим через  - логическую константу "ложь" (пустой дизъ­юнкт). Считается, что множество формул f₁, f₂, ..., f_t противоречиво (не­выполнимо), если

f₁ Ù f₂ Ù...Ù f_t ®  (7.4)

является тождественно истинной. Таким образом, если доказывается форму­ла (7.3), то тем самым устанавливается невыполнимость множества формул f₁, f₂, ..., f_t.

Из всех этих рассуждений логически следует, что невыполнимость (7.3) эквивалентна выводимости из множества формул

e₁, e₂, ..., e_n,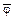

пустого дизъюнкта. Очевидно, что пустой дизъюнкт () является ре­зольвентой дизъюнктов С₁ = I и С₂ = 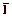, т.е. I, 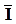^|¾ .

В качестве примера установим невыполнимость множества дизъ­юнктов:

C₁ = p Ú q;

C₂ = p Ú r;

C₃ = 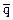Ú ;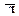

C₄ = .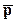

1. Резольвентой С₂ и С₄ является С₅ = r.

2. Резольвентой С₅ и С₃ является дизъюнкт С₆ =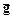

3. Резольвентой С₆ и С₁ является дизъюнкт С₇ = p.

4. Резольвентой С₄ и С₇ является пустой дизъюнкт .

Существует несколько стратегий резолюционного вывода. Проб­лема выбора эффективной стратегии связана с уменьшением длины вы­вода или, в конечном итоге, сокращением числа лишних порожденных резольвент, которые не влияют на выводимость пустого дизъюнкта. Рассмотрим две основные стратегии порождения резольвент: линейную резолюцию и семантическую резолюцию.