Эвристики поиска в дереве

Использование эвристики может привести к тому, что доказательство не будет найдено, хотя оно и существует. Однако она может значительно ускорить работу модифицированного метода поиска в глубину. В области доказательства имеется много эвристик. Обсудим некоторые из них:

А. Стратегия отбрасывания.

Говорят, что упорядоченный дизъюнкт С₁ поглощает другой упорядоченный дизъюнкт С₂, если дизъюнкт, состоящий из необрамленных литер в С₁, поглощает дизъюнкт, состоящий из необрамленных литер в С₂.

Упорядоченный дизъюнкт называется тавтологией, если он содержит контрарную пару необрамленных литер.

В модифицированном методе поиска в глубину в конце шага 4 нужно проверить, является ли R_i^*(i=1,…,m) тавтологией. Если R_i^* – тавтология, то отбрасываем его. Кроме того, следует отбросить R_i^*, если в CLIST имеется пара (С,В) такая, что R_i^* поглощается дизъюнктом С.

В. Стратегия предпочтения кратчайших дизъюнктов.

Эта стратегия вводит в модифицированный метод поиска в глубину упорядочение пар (С,В) в CLIST, чтобы лучшие пары стояли первыми. Оценивать пары рекомендуется по длине получаемого результата Length(R). Чем короче длина, тем лучше пара (С,В).

В действительности не надо вычислять R, чтобы найти ее длину, достаточно оценки: Length (R) £ Length (C) + Length (B) – 2. Смэйгл рекомендует упорядочивать пары (С,В) в списке CLIST по возрастанию.

С. Использование эвристических оценочных функций

Определим h^*(C,B) для пары (С,В), как число применений правила резолюции в минимальном доказательстве с верхним укор. дизъюнктом С и первым боковым дизъюнктом В.

Однако h^*(C,B) заранее неизвестна, поэтому введем оценку h(C,B) величины h^*(C,B). Предположим, что h(C,B) можно выразить в виде: h(C,B) = w₀+w₁f₁(C,B)+…+w_nf_n(C,B) (1), где f_i (i=1,…,n) – вещественная функция от С и В, а w_i – вес, сопоставленный величине f_i. (f_i называют характеристикой пары (С,В)).

Возможны следующие характеристики пар:

1. Число необрамленных литер в C.

2. Число обрамленных литер в С.

3. Число боковых дизъюнктов для С.

4. Число констант в последней литере из С.

5. Число функциональных символов в последней литере из С.

6. Число обрамленных литер в С, поглощающих последнюю литеру из В.

7. Число различных переменных в С и В.

8. length (C) + length (B) – 2

9. Число констант в С / (1+число переменных в С)

10. Число констант в С / (1+число различных переменных в С)

11. Глубина С.

12. Число необрамленных литер, входящих как в С, так и в В.

13. Число литер в В, имеющих обрамленное дополнение в С.

14. Число различных предикатных символов в С и В.

Функция h(C,B) может быть линейной или нелинейной от f₁(C,B),…,f_n(C,B), будем называть ее эвристической оценочной функцией, или просто оценочной функцией. Будем помещать пары (С,В) в CLIST по возрастанию значений h(C,B). Рассмотрим один из способов определения подходящих величин w₀,…,w_n.Способ определения значений множества w.

Допустим, что мы знаем величины h^*(C₁,B₁),…,h(C_q,B_q), тогда определение w₀,…,w_n таких, что минимально выражение 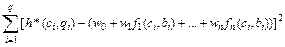(2) – оценка по наименьшим квадратам.

Определим матрицы H, F и W следующим образом:

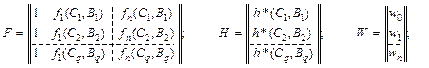
Тогда W=(F’F)^–1F’H (3),где F’ – транспонированная матрица F, (F’F)^–1 – обратная матрица к (F’F).

Рассмотрим пример. Занумеруем все дизъюнкты дерева. Используем следующие характеристики.

f₁(C,B) = length (C) + length (B) – 2

f₂(C,B) = число обрамленных литер в С

f₃(C,B) = число необрамленных литер, входящих как в С, так и в В

f₄(C,B) = число литер в В, имеющих обрамленное дополнение в С

f₅(C,B) = число обрамленных литер в С, поглощающих последнюю литеру из В

Вычисляя характеристики для любой пары дерева, получим:

i	пара	f₁(C_i,B_i)	f₂(C_i,B_i)	f₃(C_i,B_i)	f₄(C_i,B_i)	f₅(C_i,B_i)	h(C_i,B_i)*
	(1,2)
	(1,3)
	(4,6)
	(4,7)
	(5,8)
	(5,9)
	(10,14)
	(10,15)
	(11,16)
	(11,17)
	(12,18)
	(12,19)
	(13,20)
	(13,21)

Вычисляя по (3) W, получим:

w₀=0,3	w₂=0,76	w₄=–1,44
w₁=1,68	w₃=–0,24	w₅=0,6

Тогда линейная оценочная функция примет вид:

h(C,B)=0,30+1,68f₁(C,B)+0,76 f₂(C,B)–0,24 f₃(C,B)–1,44 f₄(C,B)+0,6 f₅(C,B)

Если упорядочить пары в CLIST непосредственно перед 3 шагом модифицированного метода поиска в глубину, то получим 144 ветки дерева.

Конечно, чтобы оценочная функция была хорошей,

Но нас должен волновать вопрос и о том, необходимо рассмотреть как можно больше примеров.является ли выбранное множество характеристик хорошим?

Конечно, если оценочная функция обобщается на новые примеры, то можно считать это множество хорошим, в противном случае его надо менять.

<49 505152 53 54 55 >

Дата добавления: 2016-03-05; просмотров: 610;