Алгоритм поиска кратчайших путей.
Запишем двойственную задачу по отношению к исходной (1)-(5). При этом в двойственной задаче столько же переменных, сколько ограничений в исходной, и столько же ограничений, сколько в исходной задаче переменных. Ограничения (2)-(4) записаны для каждого узла сети, поэтому в двойственной задаче будет содержаться n переменных, т.е. вектор двойственных переменных запишется:
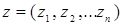 .
.
Тогда двойственная ЗЛП будет иметь вид:
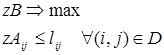 (6)
(6)
Здесь 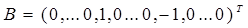 - вектор ограничений (2)-(4), в котором на r-том месте стоит 1, а на s-том стоит –1.
- вектор ограничений (2)-(4), в котором на r-том месте стоит 1, а на s-том стоит –1. 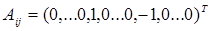 - вектор коэффициентов в ограничениях (2)-(4), в котором на i-том месте стоит 1, а на j-том стоит -1. Двойственные переменные не ограничены по знаку. В скалярной форме (6) запишется:
- вектор коэффициентов в ограничениях (2)-(4), в котором на i-том месте стоит 1, а на j-том стоит -1. Двойственные переменные не ограничены по знаку. В скалярной форме (6) запишется:
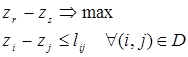 (7)
(7)
Также как и в методе потенциалов, одну из двойственных переменных можно назначить произвольно. Пусть  . Для удобства записи сделаем замену:
. Для удобства записи сделаем замену: 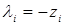 . Тогда задача (7) примет вид:
. Тогда задача (7) примет вид:
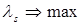 (8)
(8)
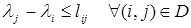 (9)
(9)
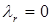 (10)
(10)
Таким образом, вместо исходной задачи (1)-(5) необходимо решить двойственную задачу (8)-(10). Для этого исходные данные записываются в следующую таблицу:
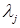
| … | 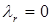
| … | … | ||||
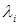
| i j | … | r | … | s | … | n | |
| … | 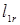
| … | 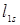
| … | 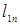
| |||
| … | … | … | … | … | ||||
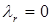
| r | 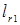
| 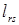
| 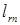
| ||||
| … | … | … | … | |||||
| n | 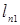
| … | 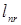
| … | 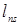
| … |
Клетки строк 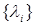 и столбцов
и столбцов 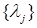 заполняются величинами
заполняются величинами 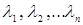 по мере решения задачи (8)-(10). Остальные клетки соответствуют дугам
по мере решения задачи (8)-(10). Остальные клетки соответствуют дугам 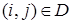 и заполняются значениями длин дуг
и заполняются значениями длин дуг 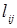 . Оставшиеся клетки не заполняются и в расчетах не участвуют.
. Оставшиеся клетки не заполняются и в расчетах не участвуют.
Вначале в строке и столбце с номерами r записываются нулевые значения 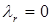 . Далее последовательно заполняются элементы столбцов
. Далее последовательно заполняются элементы столбцов 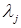 начиная с №1. Для определения элемента
начиная с №1. Для определения элемента 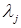 просматривается столбец №jи если в этом столбце существует хотя бы одна клетка
просматривается столбец №jи если в этом столбце существует хотя бы одна клетка 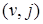 с известным элементом
с известным элементом 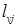 и известным значением
и известным значением 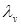 , то
, то 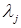 вычисляется :
вычисляется :
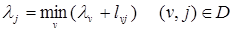
Минимум берется среди всех клеток 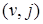 , для которых известны
, для которых известны 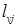 и
и 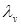 . Найденные значения записываются в строке и столбце с номером j. Этот процесс продолжается до тех пор, пока не определится
. Найденные значения записываются в строке и столбце с номером j. Этот процесс продолжается до тех пор, пока не определится 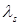 для конечного узла s искомого пути.
для конечного узла s искомого пути.
Рассматриваемый алгоритм позволяет найти кратчайшие пути из узла r до любого другого узла сети. Поэтому вычисление значений 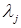 необходимо продолжать до тех пор, пока не найдутся значения всех
необходимо продолжать до тех пор, пока не найдутся значения всех 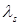 , соответствующих всем конечным узлам , до которых необходимо найти кратчайший путь из узла r.
, соответствующих всем конечным узлам , до которых необходимо найти кратчайший путь из узла r.
Если при просмотре столбцов 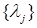 с неизвестными значениями
с неизвестными значениями 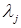 невозможно их определить, то это значит, что до этих узлов jне существует пути из узла r. Строки и столбцы, соответствующие узлу j, из таблицы вычеркиваются.
невозможно их определить, то это значит, что до этих узлов jне существует пути из узла r. Строки и столбцы, соответствующие узлу j, из таблицы вычеркиваются.
Пусть найдены все 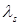 для конечных узлов
для конечных узлов 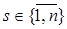 . Далее поверяются условия оптимальности (9). При этом возможны 2 случая:
. Далее поверяются условия оптимальности (9). При этом возможны 2 случая:
1. Для любых дуг 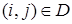 справедливо неравенство
справедливо неравенство 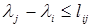 . Это означает, что кратчайшие пути найдены.
. Это означает, что кратчайшие пути найдены.
2. Существует хотя бы одна дуга 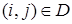 , для которой имеет место
, для которой имеет место 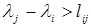 . Это означает, что решение задачи не найдено, и решение следует продолжить. Для этого в клетках столбцов
. Это означает, что решение задачи не найдено, и решение следует продолжить. Для этого в клетках столбцов 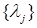 и строк
и строк 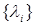 , не удовлетворяющих неравенству (9), вместо значений
, не удовлетворяющих неравенству (9), вместо значений 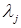 записываются исправленные значения
записываются исправленные значения 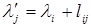 .
.
После этого условие оптимальности проверяется вновь, и процедура повторяется до тех пор, пока не будет иметь места первый случай.
Когда задача решена, то величины 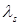 , соответствующие концам пути, определяют длину кратчайшего пути из r в s, т.е.
, соответствующие концам пути, определяют длину кратчайшего пути из r в s, т.е. 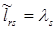 .
.
Сам кратчайший путь, т.е. узлы, через которые он проходит, восстанавливается следующим образом: в столбце s находится клетка 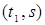 , для которой
, для которой 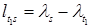 . Такая клетка обязательно существует. Дуга
. Такая клетка обязательно существует. Дуга 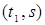 будет последним звеном искомого пути. Далее в столбце с номером
будет последним звеном искомого пути. Далее в столбце с номером 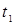 находится клетка
находится клетка 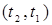 , для которой
, для которой 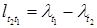 . Дуга
. Дуга 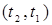 будет предпоследним звеном цепи. Далее просматривается столбец
будет предпоследним звеном цепи. Далее просматривается столбец 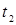 и т.д. до тех пор, пока не найдется первое звено пути
и т.д. до тех пор, пока не найдется первое звено пути 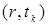 , для которого
, для которого 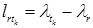 .
.
Таким образом, найден путь 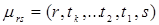 . Длина этого пути
. Длина этого пути 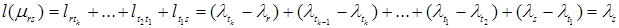
Для доказательства того, что найденный путь действительно является кратчайшим, рассматривается любой произвольный путь 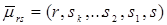 для дуг которого выполняется неравенство (9), и доказывается, что его длина
для дуг которого выполняется неравенство (9), и доказывается, что его длина 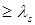 , т.е.
, т.е. 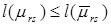 .
.
Так как предполагается, что для дуг пути 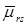 выполняются неравенства (9), то можно записать:
выполняются неравенства (9), то можно записать:
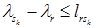
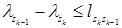
…
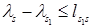
Если сложить левые и правые части этих неравенств, то можно записать 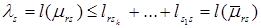 . Таким образом
. Таким образом 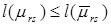 . Что и требовалось доказать.
. Что и требовалось доказать.
Пример.
Найти кратчайший путь на заданной транспортной сети из узла №3 в узлы №5 и №7.
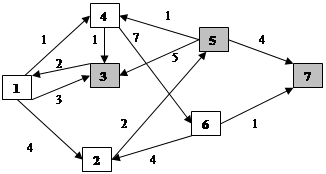 |
r=3, s=5,7.
| ||||||||
| i j | |||||||
| 4 | 3 | 1 | ||||||
| 2 | ||||||||
| 2 | ||||||||
| 1 | 7 | |||||||
| 5 | 1 | 4 | ||||||
| 4 | 1 | |||||||
Полагаем сначала 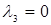 . Далее:
. Далее:
1. j=1, v=3, lvj=2. 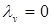 Þ
Þ 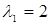 .
.
2. j=2, v=1, lvj =4. 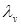 =2Þ
=2Þ 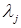 =6.
=6.
3. j=4, v=1, lvj =1. 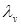 =2Þ
=2Þ 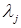 =3.
=3.
4. j=5, v=2, lvj =2. 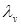 =6Þ
=6Þ 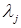 =8.
=8.
5. j=6, v=4, lvj =7. 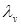 =3Þ
=3Þ 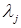 =10.
=10.
6. j=7, v1=5, 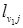 =4.
=4. 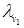 =8Þ
=8Þ 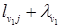 =12
=12
v2=6, 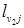 =1.
=1. 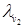 =10Þ
=10Þ 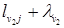 =11
=11
Þ 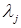 =11.
=11.
Проверка на оптимальность:
1. (1,2): 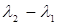 =4=
=4= 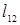 7. (4,6):
7. (4,6): 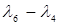 =7=
=7= 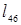
2. (1,3): 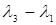 =-2<
=-2< 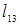 8. (5,3):
8. (5,3): 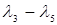 =-8<
=-8< 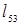
3. (1,4): 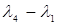 =1=
=1= 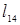 9. (5,4):
9. (5,4): 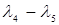 =-5<
=-5< 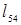
4. (2,5): 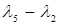 =2=
=2= 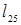 10. (5,7):
10. (5,7): 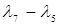 =3<
=3< 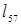
5. (3,1): 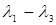 =2=
=2= 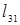 11. (6,2):
11. (6,2): 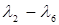 =-8<
=-8< 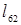
6. (4,3): 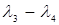 =-3<
=-3< 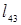 12. (6,7):
12. (6,7): 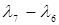 =1=
=1= 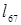
Условие оптимальности выполняется для всех 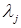 . Длина пути
. Длина пути 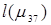 =
= 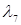 =11,
=11, 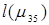 =
= 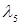 =8.
=8.
Восстановление пути:
1. Путь 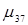 : (3,1,4,6,7)
: (3,1,4,6,7)
2. Путь 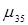 (3,1,2,5).
(3,1,2,5).
| <== предыдущая лекция | | | следующая лекция ==> |
| Диэлектрические свойства сегнетоэлектриков | | | Сущностные характеристики опасных и чрезвычайных ситуаций социального происхождения |
Дата добавления: 2016-04-02; просмотров: 1303;
