Алгоритм Берленкемпа-Месси.

Пусть P – некоторое поле, e – единица поля P. Обозначим через 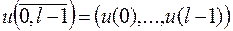начальный отрезок произвольной последовательности u элементов поля P. Будем говорить, что многочлен

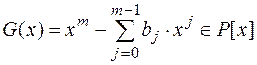
вырабатывает отрезок 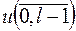, если

,

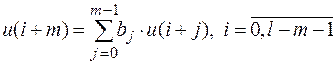то есть данный отрезок последовательности является отрезком некоторой линейной рекуррентной последовательности с характеристическим многочленом G(x). Алгоритм Берленкемпа-Месси строит многочлен G(x) наименьшей степени, вырабатывающий отрезок .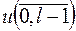

Определим функцию умножения последовательности на многочлен. Для произвольного многочлена 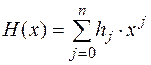и последовательности v положим H(x) · v = w, где

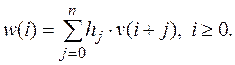
Многочлен G(x) вырабатывает l ³ m знаков последовательности u, если выполняется равенство

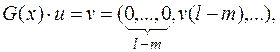
то есть если первые l – m знаков последовательности v равны нулю, а следующий за ними отличен от нуля.

Для многочлена G(x) Î P[x] степени m и последовательности u введем параметры l_u(G) и k_u(G) = l_u(G) – m Î N È {0, +¥}, где l_u(G) – число знаков последовательности u, вырабатываемых многочленом G(x). Ясно, что k_u(G) – максимальное число первых подряд идущих нулей в последовательности G(x) · u (либо ¥).

Будем индуктивно строить последовательность многочленов G₀(x), G₁(x), … неубывающих степеней 0 = m₀ < m₁ £ m₂ £ … .

Начальные условия: G₀(x) = e, m₀ = 0.

Этап 1. Если

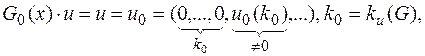
то полагаем

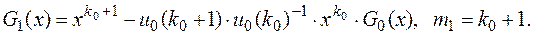
Если G₁(x)·u = 0, то есть если k_u(G₁) = ¥, то G₁(x) – искомый минимальный многочлен ЛРП u. В противном случае строим G₂(x).

Этап t + 1. пусть многочлены G₀(x), …, G_t(x) уже построены, и степень многочлена G_j(x) равна m_j, причем 0 = m₀ < m₁ £ m₂ £ … m_t. Пусть выполняются соотношения

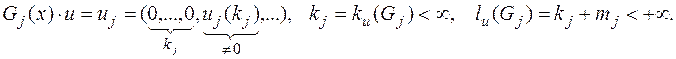Определим число s = s(t) так, чтобы выполнялись условия m_t = m_t - 1 = … = m_s + 1 > m_s (такое s найдется, так как m₁ > m₀). Положим

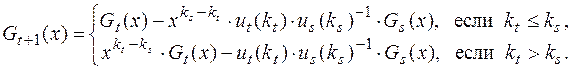
Если G_t+1(x)·u = 0, то нужный многочлен построен. В противном случае строим G_t+2(x).

Теорема: Если u – линейная рекуррентная последовательность над полем P с минимальным многочленом степени m, то F(x) = G_t(x) для некоторого подходящего значения t £ 2m – 1 – k₀.