VI. Методы и алгоритмы проверки выводимости.
Пусть задана совокупность ППФ 
, которая называется посылками (иногда гипотезами), и ППФ – 
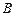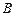. « » называется логическим следствием . или выводимой из А (записывается как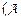 
⊦ 
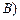), если 
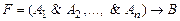является тавтологией (тождественно истинным высказыванием).
Таким образом, задача проверки выводимости сводится к проверке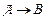 
на тождественную истинность. Существует несколько десятков методов и алгоритмов установления тождественной истинности логической формулы.
1. Алгоритм истинностных таблиц (АИТ) для F=A®B.
АИТ сводится к последовательной подстановке всех возможных интерпретаций (наборов «истина» и «ложь») переменных, входящих в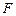 
. Алгоритм останавливается, если значение 
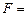ложь ( 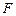не выполнима, а значит 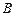не выводима из 
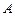на всех интерпретациях); 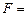истина ( 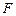выполнима на всех интерпретациях, значит 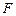суть тавтология и А⊦ 
. Такой алгоритм требует в наихудшем случае 2n подстановок (2n возможных интерпретаций), где «n» число переменных, входящих в формулу F.
2. Алгоритм Квайна(Квайн. 1960 г. США)
Идея: при последовательных подстановках значений переменных можно уменьшить длину формулы, исходя из совокупности проведённых проверок истинности F, и тем самым сокращать число переменных для проверки.
Вводится понятие дерева испытаний, которое по сути дела представляет собой граф всех интерпретаций проверяемой формулы 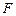. Квайн назвал его «семантическим деревом».
Пример: Пусть необходимо проверить общезначимость формулы
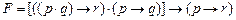
Семантическое дерево. Каждое левое ребро дерева соответствует переменным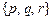 
, а каждое правое ребро – 
.
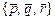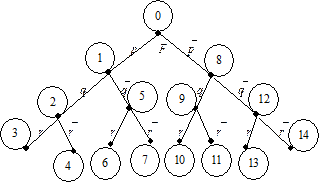
Каждая ветвь (например, самая левая) соответствует набору (p×q×r), самая правая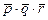 
. Дерево перечисляет все возможные элементарные конъюнкции.
1) Положим для F (вершина )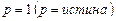 
, тогда
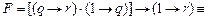(напомним, что 
–
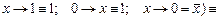
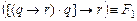(формула в вершине «1»)
2) Положим для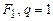 
, тогда
. 
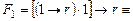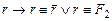
(формула в вершине «2»)
 |
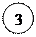3) 
Спустимся до вершины . Положим для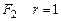 
, тогда значение 
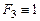(формула в вершине «3»).
4) Поднимемся к вершине , в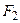 
положим 
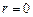, тогда 
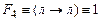(формула в вершине «4»).
Поднимемся к вершине и в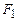 
положим 
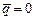, следуя нумерации вершин, находим, что 
. 
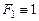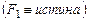. Можно заметить характерное правило обхода вершин.
Такой алгоритм обхода вершин семантического дерева называется алгоритмом с возвратом (back tracking). На рисунке показан путь обхода семантического дерева. В процессе обхода вычисляется значение формулы F. Оказывается, что на всех наборах значений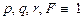 
. Таким образом F является тавтологией.
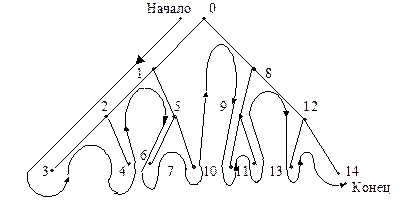
3. Метод резолюций (Д.Робинсон, 1965 г., США).
Алгоритмы доказательства выводимости А⊦B, построенные на основе этого метода, применяются во многих системах искусственного интеллекта, а также являются фундаментом, на котором построен язык логического программирования «Пролог».
Метод резолюций использует несколько принципов.
Дата добавления: 2016-03-22; просмотров: 2409;