Алгоритмы сортировки и поиска

14.5.1. Сортировка

Сортировка (то есть упорядочение по возрастанию или убыванию значений в списках, массивах, записях и других последовательностях элементов) является одной из наиболее важных алгоритмических задач, непосредственно связанных с проблемами эффективного управления, поиска и извлечения информации. Известны следующие распространенные методы сортировки:

□ сортировка вставками;

□ пузырьковая сортировка;

□ сортировка Шелла;

□ корневая сортировка;

□ пирамидальная сортировка;

□ сортировка слиянием;

□ быстрая сортировка.

Сортировка вставками

Основная идея сортировки вставками состоит в том, что при добавлении ново­го элемента в уже отсортированный список его сразу вставляют в нужное место вместо того, чтобы вставлять его в произвольное место, а затем заново сортировать весь список. При сортировке вставками первый элемент любого списка считается отсортированным списком длины 1. Двухэлементный отсортированный список создается добавлением второго элемента исходного списка в нужное место одно­элементного списка, содержащего первый элемент. После этого можно вставить третий элемент исходного списка в отсортированный двухэлементный список. Этот процесс повторяется до тех пор, пока все элементы исходного списка не окажутся в расширяющейся отсортированной части списка.

Пузырьковая сортировка

Основной принцип пузырьковой сортировки состоит в выталкивании меньших значений на вершину списка, в то время как большие значения опускаются вниз.

Алгоритм пузырьковой сортировки приведен на рис. 14.32. У пузырьковой со­ртировки есть много различных вариантов. В алгоритме пузырьковой сортировки совершается несколько проходов по списку. При каждом проходе происходит срав­нение соседних элементов. Если порядок соседних элементов неправильный, то они меняются местами. Каждый проход начинается с начала списка. Сперва сравнива­ются первый и второй элементы, затем — второй и третий, потом — третий и чет­вертый, и т. д.; элементы с неправильным порядком в паре переставляются. При обнаружении на первом проходе наибольшего элемента списка он переставляется со всеми последующими элементами, пока не дойдет до конца списка. Поэтому при втором проходе нет необходимости производить сравнение с последним элементом.

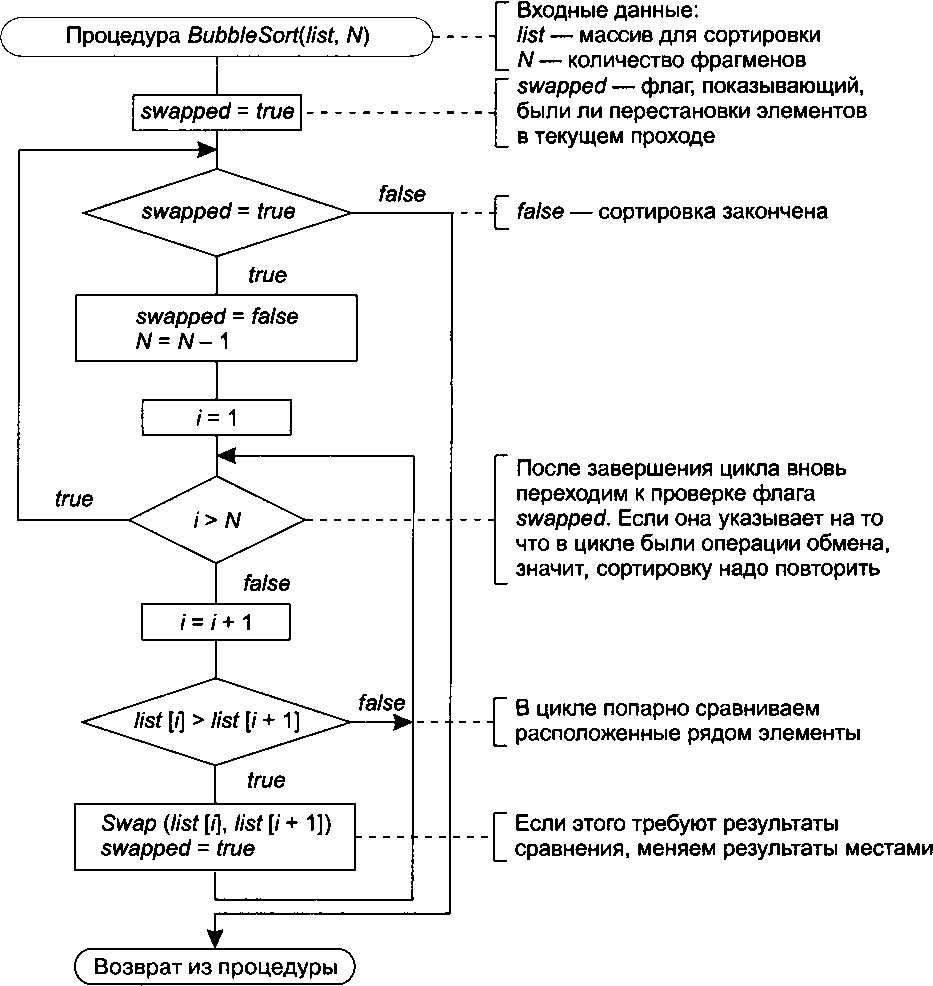Рис. 14.32. Алгоритм пузырьковой сортировки

При втором проходе второй по величине элемент списка опускается во вторую* позицию с конца. При продолжении процесса на каждом проходе по крайней мере одно из следующих по величине значений встает на свое место. При этом меньшие значения тоже собираются наверху. Если при каком-то проходе не происходит ни одной перестановки элементов, это означает, что все они стоят в нужном порядке, и исполнение алгоритма можно прекратить. Стоит заметить, что при каждом про­ходе ближе к своему месту продвигается сразу несколько элементов, хотя гаран­тированно занимает окончательное положение лишь один.

Сортировка Шелла

Суть сортировки Шелла состоит в том, что весь список рассматривается как совокупность перемешанных подсписков. На первом шаге эти подсписки представ­ляют собой просто пары элементов. На втором шаге в каждой группе оказывается по четыре элемента. При повторении процесса количество элементов в каждом подсписке увеличивается, а количество подсписков, соответственно, падает.

Корневая сортировка

При корневой сортировке упорядочивание списка происходит без непосред­ственного сравнения ключевых значений между собой. При этом создается набор «стопок», а элементы распределяются по стопкам в зависимости от значений клю­чей. Собрав значения обратно и повторив всю процедуру для последовательных частей ключа, можно получить отсортированный список. Чтобы такая процедура работала, распределение по стопкам и последующую сборку следует выполнять очень аккуратно.

Пирамидальная сортировка

В основе пирамидальной сортировки лежит специальный тип бинарного дерева, называемый пирамидой; значение корня в любом поддереве такого дерева больше, чем значение каждого из его потомков. Непосредственные потомки каждого узла не упорядочены, поэтому иногда левый непосредственный потомок оказывается больше правого, а иногда наоборот. Пирамида представляет собой полное дерево, в котором заполнение нового уровня начинается только после того, как преды­дущий уровень оказывается заполненным целиком, а все узлы на одном уровне заполняются слева направо.

Сортировка начинается с построения пирамиды. При этом максимальный элемент списка оказывается в вершине дерева: ведь потомки вершины обяза­тельно должны быть меньше. Затем корень записывается последним элементом списка, а пирамида с удаленным максимальным элементом переформировывает­ся. В результате в корне оказывается второй по величине элемент, он копируется в список, и процедура повторяется, пока все элементы не окажутся возвращенными в список.

Сортировка слиянием

Сортировка слиянием — один из распространенных алгоритмов рекурсивной сортировки. В ее основе лежит замечание, согласно которому слияние двух от­сортированных списков выполняется быстро. Список из одного элемента уже отсортирован, поэтому при сортировке слиянием список разбивается на одноэле­ментные куски, которые затем постепенно сливаются. Поэтому вся деятельность заключается в слиянии двух списков.

Быстрая сортировка

Быстрая сортировка — один из наиболее популярных алгоритмов рекурсивной сортировки. При быстрой сортировке после выбора в списке элемента список с его помощью делится на две части. В первую часть попадают все элементы, меньшие выбранного, во вторую — большие выбранного. В среднем такая сортировка эффек­тивна, однако в наихудшем случае ее эффективность такая же, как у сортировки вставками и у пузырьковой сортировки.

При быстрой сортировке в списке выбирается элемент, называемый осевым, а затем список переупорядочивается таким образом, что все элементы, меньшие осевого, оказываются перед ним, а большие элементы — за ним. В каждой из ча­стей списка элементы не упорядочиваются. Если п — окончательное положение осевого элемента, то нам известно лишь, что все значения в позициях с первой по п- 1 меньше осевого, а значения с номерами от п + 1 до N- больше осевого. Далее алгоритм вызывается рекурсивно на каждой из двух частей.

14.5.2. Поиск

Под алгоритмами поиска понимается процесс просмотра списка в поисках некоторого конкретного элемента, называемого целевым. При последовательном поиске всегда предполагается, что список не отсортирован, поскольку некоторые алгоритмы на отсортированных списках показывают лучшую производительность. Обычно поиск производится не просто для проверки того, что нужный элемент в списке имеется, а и для того, чтобы получить данные, относящиеся к этому зна­чению ключа. Например, ключевое значение может быть номером сотрудника, порядковым номером или любым другим уникальным идентификатором. После того как нужный ключ найден, программа может, например, частично изменить связанные с ним данные или просто вывести всю запись. Во всяком случае, перед алгоритмом поиска стоит важная задача определения местонахождения ключа. Поэтому алгоритмы поиска возвращают индекс записи, содержащей нужный ключ. Если ключевое значение не найдено, то алгоритм поиска обычно возвращает зна­чение индекса, превышающее верхнюю границу массива. Положим, что элементы списка имеют номера от 1 до N. Это позволит возвращать 0 в случае, если целевой элемент отсутствует в списке. Для простоты предполагаем, что ключевые значения не повторяются.

Последовательный поиск

В алгоритме последовательного поиска последовательно просматривается по одному элементу списка, начиная с первого, до тех пор, пока не будет найден це­левой элемент. Очевидно, что чем дальше в списке находится конкретное значение

ключа, тем больше времени уйдет на его поиск. Это следует помнить при анализе алгоритма последовательного поиска.

Полный алгоритм последовательного поиска показан на рис. 14.33.

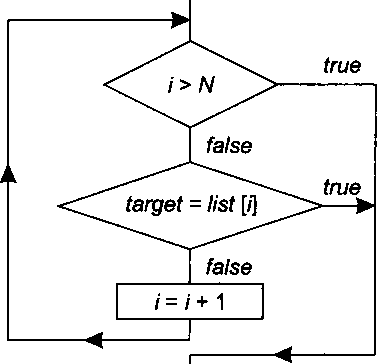Q Конец )

Входные данные:

list — массив для поиска (индексы от 1 до Л/) N — количество элементов (Л/ > 0) target— искомый элемент Выходные данные: / — индекс искомого элемента, если _i = N + 1 — элемент не найден

Рис. 14.33. Алгоритм последовательного поиска

Двоичный поиск

При сравнении целевого значения со средним элементом отсортированного списка возможен один из трех результатов: значения равны, целевое значение меньше элемента списка, целевое значение больше элемента списка. В первом, и наилучшем, случае поиск завершен. В остальных двух случаях можно отбросить половину списка. Когда целевое значение меньше среднего элемента, известно, что если оно имеется в списке, то находится перед этим средним элементом. Ког­да же оно больше среднего элемента, известно, что если оно имеется в списке, то находится после этого среднего элемента. Этой информации достаточно, чтобы стало возможно одним сравнением отбросить половину списка. При повторении этой процедуры можно отбросить половину оставшейся части списка. Очевидно, что такой алгоритм будет работать только на предварительно отсортированном списке.

Вопросы для самопроверки

1. Откуда произошел термин «алгоритм»?

2. Чем численный алгоритм отличается от логического?

3. Из каких разделов состоит современная теория алгоритмов?

4. Дайте определение алгоритма по Маркову.

5. Дайте определение алгоритма по Колмогорову.

6. Каким требованиям должен отвечать алгоритм?

7. Что собой представляет машина Поста?

8. Что собой представляет машина Тьюринга?

9. Какие способы записи алгоритмов вам известны?

10. Каковы недостатки словесного способа записи алгоритма?

11. Каковы достоинства и недостатки представления алгоритма в виде блок-схемы?

12. Приведите пример простейшего алгоритма, представленного при помощи диа­граммы Нэсси—Шнейдермана.

13. Что такое «псевдокоды»?

14. На какие группы можно подразделить языки программирования высокого уровня?

15. Какие базовые алгоритмические конструкции вам известны?

16. Что такое «линейный алгоритм»?

17. Что такое «разветвляющийся алгоритм»? Чем обуславливается выбор пути при ветвлении?

18. Что такое «циклический алгоритм»? Чем отличается цикл с предусловием от цикла с постусловием?

19. Дайте определение данным. Чем данные отличаются от переменных и кон­стант?

20. Какие базовые типы данных вам известны?

21. Что такое «массив»?

22. Что такое «запись»?

23. Что такое «связный список»? «Односвязньш список»? «Двусвязный список»?

24. Опишите в словесной форме алгоритм удаления элемента односвязного списка.

25. Опишите в форме псевдокода алгоритм удаления элемента двусвязного списка.

26. Что такое «деревья»?

27. Что такое «корневое дерево»? Что такое «корень дерева»?

28. Что такое «бинарное дерево»?

29. Что такое «граф»?

30. Чем различаются ориентированный и не ориентированный графы?

31. В решении каких задач применяются графы?

32. Какие алгоритмы сортировки вам известны? Опишите особенности каждого из них.

33. Какие алгоритмы поиска вам известны?

Литература

1. Голицына О. JI., Попов И. И. Основы алгоритмизации и программирования. M.: Форум, 2008.

2. Давыдов В. Г. Программирование и основы алгоритмизации. M.: Высшая школа, 2003.

3. Кузюрин Н. H., Фомин С. А. Эффективные алгоритмы и сложность вычислений. Электронное издание, http://discopal.ispras.ru/ru.book-advanced-algorithms.htm

4. Мозговой М. В. Классика программирования: алгоритмы, языки, автоматы, ком­пиляторы. Практический подход. СПб.: Наука и техника, 2006.