Алгоритм пирамидальной сортировки (HeapSort)

В некоторых приложениях (например, в задачах управления оборудованием в реальном времени) крайне важно иметь гарантию, что время работы критических ветвей программы даже в самом плохом случае не превысит некоторой заданной величины. Для таких задач использование QuickSort может оказаться неприемлемым ввиду названного выше недостатка этого алгоритма – времени работы порядка O(n²) в худшем случае. В этой ситуации следует использовать такой алгоритм, который работает гарантированно быстро даже в худшем случае.

Наиболее известным из таких алгоритмов является HeapSort, который по-русски принято называть пирамидальной сортировкой.

В основе алгоритма лежит понятие пирамиды.

Массив A называется пирамидой, если для всех его элементов выполнены следующие неравенства:

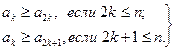(3.1)

Смысл неравенств (3.1) можно наглядно пояснить на рис. 3.1.

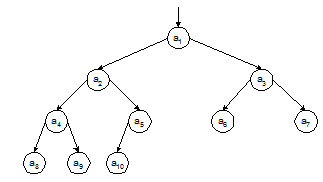
Рис. 3.1. Представление пирамиды в виде дерева

На рисунке массив-пирамида из 10 элементов изображен в виде сбалансированного бинарного дерева, вершины которого пронумерованы сверху вниз и слева направо. При этом элемент a_k всегда будет в дереве «отцом» элементов a_2k и a_2k+1 (если такие элементы имеются). Тогда неравенства (3.1) означают, что значение «отца» должно быть не меньше, чем значения каждого из «сыновей».

Следует, однако, помнить, что пирамида – это не дерево, а массив с определенными свойствами, а изображение пирамиды в виде дерева дано только для наглядности.

Пирамида вовсе не обязательно является сортированным массивом, однако она служит удобным промежуточным результатом при сортировке. Отметим, что первый элемент пирамиды (a₁) всегда является максимальным элементом массива.

Работа алгоритма HeapSort состоит из двух последовательных фаз. На первой фазе исходный массив перестраивается в пирамиду, а на второй фазе из пирамиды строится сортированный массив.

Основной операцией, используемой как на первой, так и на второй фазах сортировки, является так называемое просеивание элемента сквозь пирамиду.

Предположим, что неравенства (3.1) выполнены для элементов пирамиды, начиная с индекса k+1 (т.е. для элементов a_k+1, a_k+2, … , a_n). Процедура просеивания элемента a_k должна обеспечить выполнение (3.1) для a_k и при этом не нарушить этих неравенств для a_k+1, a_k+2, … , a_n.

Алгоритм просеивания заключается в следующем.

1. Если a_k не имеет сыновей (т.е. 2k > n), то просеивание закончено.

2. Если a_k имеет ровно одного сына (т.е. 2k = n), то присвоить l := n и перейти к шагу 4.

3. Сравнить значения двух сыновей вершины a_k: если a_2k > a_2k+1, то l := 2k, иначе l := 2k + 1 (т.е. l – это индекс большего из сыновей a_k).

4. Сравнить значения элемента a_k со значением его большего сына a_l: если a_k < a_l, то поменять местами a_k и a_l.

5. Присвоить k := l и перейти к шагу 1.

На рис. 3.1 выполнение просеивания выглядит следующим образом: вершина дерева, значение которой меньше значения хотя бы одного из ее сыновей, опускается вдоль одной из ветвей дерева, пока не займет свое законное место. При этом все остальные вершины дерева за пределами этой ветви остаются неизменными[2].

Нетрудно видеть, что максимально возможное число повторений цикла в процедуре просеивания не превышает log₂n (поскольку на каждой итерации значение k увеличивается по крайней мере в 2 раза).

Теперь нетрудно описать алгоритм сортировки HeapSort в целом, используя понятие просеивания элемента.

Первая фаза алгоритма (построение пирамиды) начинается с вычисления наибольшего индекса элемента a_k, у которого есть хотя бы один сын. Очевидно, k := n div 2. Затем выполняется просеивание элементов a_k, a_k–1, a_k–2, …, a₂, a₁. На этом построение пирамиды завершено.

Вторая фаза алгоритма (построение сортированного массива) состоит из следующих шагов.

1. Поменять местами элементы a₁ и a_n. Напомним, что в пирамиде a₁ – максимальный элемент; после обмена он будет стоять на последнем месте.

2. Присвоить n := n - 1. Тем самым мы как бы исключаем последний элемент из пирамиды и включаем его в сортированный массив, который должен быть результатом работы алгоритма.

3. Поскольку после обмена для нового элемента a₁ могло нарушиться свойство (3.1), выполнить просеивание a₁. После этого на месте a₁ окажется максимальный из оставшихся элементов пирамиды.

4. Если n > 1, то перейти к шагу 1, иначе сортировка завершена.

На каждой итерации второй фазы происходит исключение из пирамиды максимального из оставшихся в ней элементов. Этот элемент записывается на подобающее ему место в сортированном массиве. К концу работы алгоритма вся пирамида превращается в сортированный массив.

Оценим время работы каждой фазы алгоритма HeapSort. Первая фаза состоит из n/2 операций просеивания, каждая из которых включает не более log₂(n) итераций цикла. Отсюда можем легко получить для первой фазы оценку T_макс(n) = O(n×log(n)). Однако эта оценка чересчур грубая. В дальнейшем нам понадобится более точная оценка времени работы первой фазы HeapSort. Чтобы получить такую оценку, рассмотрим рис. 3.2.

Рис. 3.2. Число итераций просеивания при построении пирамиды

Из числа всех n элементов массива A примерно половина (n/2) не имеет сыновей и не требует просеивания (т.е. число итераций просеивания равно 0). Четверть элементов (n/4) имеет сыновей, но не имеет внуков, для этих элементов может быть выполнено не больше одной итерации просеивания. Для одной восьмой части элементов (n/8) могут быть выполнены две итерации, для одной шестнадцатой (n/16) – три итерации и т.д. Суммарное число итераций просеивания определится формулой: n (0×1/2 + 1×1/4 + 2×1/8 + 3×1/16 + …). Тряхнув воспоминаниями о матанализе, можно вычислить значение суммы ряда в скобках; это значение равно 1. Таким образом, получаем линейную оценку времени для первой фазы: T_макс(n) = O(n).

Вторая фаза алгоритма в основном представляет собой просеивание элементов сквозь уменьшающуюся пирамиду. Число итераций цикла можно примерно оценить как сумму log₂(n) + log₂(n–1) + log₂(n–2) + … + log₂(3) + log₂(3). Поверим без доказательства, что с точностью до O-большого эта сумма дает T_макс(n) = O(n×log(n)).

Время работы алгоритма в целом определяется более трудоемкой второй фазой и удовлетворяет оценке T_макс(n) = O(n×log(n)). Можно доказать, что такая же оценка справедлива и для среднего времени сортировки: T_ср(n) = O(n×log(n)). Таким образом, HeapSort представляет собой алгоритм сортировки, который гарантирует достаточно быструю работу даже в случае самых неудачных исходных данных. Этим HeapSort выгодно отличается от QuickSort, который такой гарантии не дает. С другой стороны, практика показывает, что в среднем алгоритм HeapSort работает примерно вдвое медленнее, чем QuickSort.