Задача внешней сортировки

Все ранее рассматривавшиеся алгоритмы сортировки были ориентированы на работу с массивом, полностью помещающемся в оперативной памяти компьютера. Между тем, несмотря на постоянное возрастание емкости памяти современных компьютеров, не теряют своей актуальности задачи сортировки и поиска в больших наборах данных, которые хранятся в файлах и не могут быть полностью считаны в оперативную память. В частности, подобные задачи возникают при работе систем управления базами данных.

Задача сортировки данных, расположенных во внешней памяти и только по частям считываемых в оперативную память, называется задачей внешней сортировки (в отличие от задачи внутренней сортировки, которую мы рассматривали до сих пор).

Формально говоря, любой из описанных алгоритмов может быть применен и к задаче внешней сортировки. Это возможно хотя бы потому, что современные операционные системы позволяют работать с файлами как с виртуальными массивами, т.е. обращаться к их записям по индексу, возложив на систему планирование и выполнение операций чтения и записи данных на внешнее устройство. Однако попытка применить, например, QuickSort или HeapSort для сортировки файла вызовет катастрофическое замедление работы, как только файл перестанет целиком помещаться в оперативной памяти, отведенной программе.

Это связано с тем, что алгоритмы внутренней сортировки оптимизированы по количеству операций, выполняемых над данными в оперативной памяти, прежде всего операций сравнения ключей и операций присваивания (перестановки) записей. Делая оценки эффективности алгоритмов, мы подсчитывали количество итераций циклов, а основным содержанием каждой итерации были как раз сравнения и присваивания.

Как известно, операции обмена с внешней памятью (т.е. чтения и записи на устройства) выполняются во много раз медленнее. При этом надо учитывать не только более низкую скорость передачи данных, но и существенное замедление работы при поиске требуемого блока данных (сектора диска). Поэтому при оценке алгоритмов внешней сортировки следует подсчитывать в первую очередь количество операций обращения к устройству, а операциями, выполняемыми в оперативной памяти, можно в большинстве случаев вообще пренебречь.

Если с этой точки зрения посмотреть на алгоритмы QuickSort, HeapSort и ShellSort, то картина окажется невеселой. Все эти алгоритмы резво скачут из конца в конец сортируемого массива, обеспечивая высокую эффективность прежде всего за счет дальних пересылок элементов. Для этих алгоритмов чуть ли не каждое обращение к элементу массива может потребовать выполнения операции чтения или записи в файл.

Совершенно по-другому ведет себя сортировка слиянием.

Обычно этот алгоритм для файлов реализуют как чередование двух фаз работы: фазы разделения и фазы слияния (рис. 3.3).

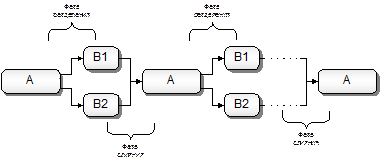
Рис. 3.3. Двухфазное слияние файлов

На фазе разделения исходный файл A просматривается от начала до конца и из него выделяются серии записей, упорядоченные по возрастанию. Нечетные по счету серии записываются во вспомогательный файл B1, четные – в файл B2.

На фазе слияния просматриваются файлы B1 и B2, прочитанные из них серии попарно сливаются и записываются в файл A.

Фазы разделения и слияния повторяются до тех пор, пока в A не будет записана единственная серия, содержащая все элементы в отсортированном виде.

Число проходов разделения/слияния может быть значительно сокращено, если на первом проходе сразу после чтения очередной порции данных из файла выполнить внутреннюю сортировку этой порции любым эффективным алгоритмом (например, QuickSort). Это будет эквивалентно созданию очень длинных возрастающих серий, размер которых ограничен только доступным объемом оперативной памяти.

Чтение и запись файлов как на фазе разделения, так и на фазе слияния выполняется только последовательно, от начала к концу. Эта особенность алгоритмов слияния была особенно важна в старые времена, когда основным видом внешних носителей данных были магнитные ленты. Однако и при работе с устройствами произвольного доступа (дисками) желательно как можно меньше пользоваться этим самым произвольным доступом, поскольку он приводит к слишком частым перемещениям читающих головок и, следовательно, к замедлению работы.

Основной недостаток алгоритмов слияния – потребность во вспомогательном массиве – для случая сортировки файлов выступает как потребность в двух вспомогательных файлах B1 и B2, суммарный размер которых равен размеру сортируемого файла. Конечно, это не очень приятное свойство, однако дисковое пространство обычно является менее дефицитным ресурсом, чем оперативная память.

Оценка эффективности методов внешней сортировки «в смысле O-большое», приводит к результату, на первый взгляд парадоксальному. Одна и та же оценка T(n) = O(n×log(n)) получается и для «подходящего» MergeSort, и для «неподходящего» QuickSort. Но здесь надо вспомнить, что оценка с точностью до O-большого характеризует только скорость роста времени при увеличении n, конкретные же значения T(n) очень сильно различаются для разных алгоритмов. В первом приближении можно считать, что для алгоритмов слияния значение n как бы делится на число записей таблицы, помещающихся в одном секторе диска.