Бинарные деревья поиска
Напомним, что под бинарным деревом понимается такая структура данных, которая либо является пустой, либо состоит из вершины, называемой корнем дерева и связанной с двумя другими бинарными деревьями, называемыми левым и правым сыновьями корня.
Мы будем рассматривать такие бинарные деревья, у которых с каждой вершиной связано значение этой вершины. Это значение может в общем случае состоять из поля ключа и поля данных, т.е. бинарное дерево можно рассматривать как иное представление таблицы, отличное от более привычного ее представления в виде массива. Как и раньше, мы для простоты будем считать, что значение вершины содержит только ключ.
Бинарным деревом поиска называется такое бинарное дерево, у которого для каждой вершины A все значения вершин левого поддерева A не превышают значения A, а все значения вершин правого поддерева A не меньше, чем значение A.
По-другому можно сказать, что бинарное дерево поиска – это такое дерево, при обходе которого слева направо значения вершин будут перечисляться в порядке возрастания.
Поиск ключа по бинарному дереву имеет много общего с процедурой бинарного поиска в массиве. В том и другом случае после проверки на совпадение с искомым ключом одного из значений (раньше это было значение из середины массива, теперь – значение корня дерева) выполняется переход либо к меньшим, либо к большим значениям ключей. Разница в том, что вместо вычисления индекса следующего проверяемого элемента здесь просто выполняется переход либо к левому, либо к правому сыну проверенной вершины.
Опишем структуры данных для представления таблицы в виде бинарного дерева.
type
Tree = ^Node; {Дерево есть указатель на его корень}
Node = record {Вершина дерева}
key: KeyType; {Ключ}
left, right: Tree; {Два сына (поддерева)}
end;
Функция поиска по дереву со вставкой может в рекурсивном варианте выглядеть, как показано ниже.
function TreeSearch(
var t: Tree; {Корень дерева}
x: KeyType; {Искомый ключ}
var found: Boolean {Найдено или вставлено?}
): Tree; {Возвращает указатель на вершину}
begin
if t = nil then begin {Вставка новой вершины}
found := false; {Не найдено, будет вставлено}
New(t);
t^.left := nil;
t^.right := nil;
t^.key := x;
TreeSearch := t;
end
else if t^.key < x then
TreeSearch := TreeSearch(t^.right, x, found)
else if t^.key > x then
TreeSearch := TreeSearch(t^.left, x, found)
else begin {t^.key = x}
found := true; {Найдено!}
TreeSearch := t;
end;
end; {TreeSearch}
Пока значение ключа текущей вершины не равно искомому, функция выполняет спуск по дереву, переходя к левому или правому сыну вершины. Спуск заканчивается либо когда будет найден искомый ключ, либо когда очередное поддерево оказывается пустым. Это означает, что искомый ключ отсутствует в дереве и должен быть вставлен в соответствующем месте. Значением функции будет указатель на найденную либо вставленную вершину.
Если функция выполнит вставку новой вершины, то исходное дерево изменится, однако оно сохранит свойства дерева поиска.
Время работы функции определяется числом шагов спуска по дереву выполненных при поиске. Время выполнения вставки не зависит от размеров дерева, поэтому оно не повлияет на оценку в смысле O-большое.
Максимальное число шагов спуска ограничено высотой дерева поиска. Как связана высота h с числом вершин дерева n? Это зависит от распределения вершин в дереве.
Наиболее предпочтительным для поиска видом деревьев являются идеально сбалансированные деревья (ИС-деревья). Это такие бинарные деревья, у которых для каждой вершины количества вершин в ее левом и правом поддеревьях различаются не больше, чем на 1. Легко доказать, что длины всех ветвей ИС-дерева также различаются не более, чем на 1.
Примеры ИС-деревьев поиска с разным числом вершин показаны на рис. 4.1.
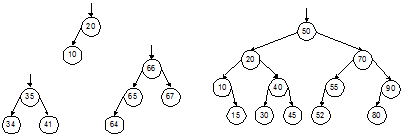
Рис. 4.1. Примеры идеально сбалансированных деревьев поиска
Нетрудно доказать, что ИС-дерево высоты h может иметь от 2h–1 до 2h – 1 вершин. Отсюда можно получить и обратную зависимость – оценку высоты для данного числа вершин: h £ log2n + 1. Получается, что время поиска по ИС-дереву имеет логарифмическую оценку: T(n) = O(log(n)), аналогично бинарному поиску в сортированном массиве.
Проблема заключается в том, что сбалансированность дерева обеспечить трудно. Предположим, что на вход программы, строящей бинарное дерево поиска с помощью функции TreeSearch, поступает монотонно возрастающая последовательность ключей. Нетрудно видеть, что в этом случае каждая новая вершина будет включаться в дерево как правый сын предыдущей вершины, а левых сыновей в этом дереве не будет вовсе. Результатом будет крайне несбалансированное вырожденное дерево, по сути представляющее собой линейный список. Для вырожденного дерева его высота равна числу вершин, а стало быть, T(n) = O(n).
С другой стороны, пусть нам удалось каким-то образом построить ИС-дерево из n вершин. Если затем в это дерево будет добавлено еще хотя бы 1-2 вершины, то его балансировка может быть нарушена и для ее восстановления придется заново строить все дерево, затратив на это время порядка O(n).
Таким образом, для несбалансированного дерева время порядка O(n) может тратиться на каждый поиск ключа, а для идеально сбалансированного аналогичное время будет затрачиваться на процедуру перебалансировки после добавления вершины.
Разумеется, вырожденное дерево – это заведомо худший случай. В среднем дело обстоит не так плохо. Доказано, что если вершины добавляются в случайном порядке, то математическое ожидание высоты получившегося дерева будет иметь логарифмическую оценку и лишь примерно на 40 % превысит высоту ИС-дерева с тем же количеством вершин.
Ситуация напоминает ту, которая характерна для алгоритма QuickSort: в среднем все очень хорошо, но не исключен и худший случай, когда все становится плохо.
До сих пор мы говорили только о добавлении вершин (записей) в бинарное дерево поиска. Выполнение удаления вершин несколько сложнее, поскольку нужно уметь удалять не только листья, но и внутренние вершины дерева, и при этом нужно обеспечить сохранение целостности дерева. Не вдаваясь в подробности, покажем на рис. 4.2, как выполняется удаление на примере разных вершин одного и того же дерева.
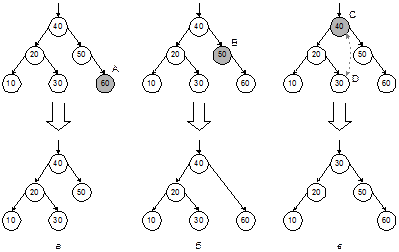
Рис. 4.2. Удаление вершин из дерева поиска
На рис. 4.2, а показано удаление вершины A, не имеющей сыновей. Здесь проблем не возникает.
На рис. 4.2, б иллюстрируется удаление вершины B, имеющей одного сына. При этом у отца удаляемой вершины освобождается одна связь, к которой и присоединяется «осиротевший внук». Очевидно, что сортированность дерева поиска при этом сохраняется.
На рис. 4.2, в показан самый сложный случай – удаление вершины C, имеющей двух сыновей. Чтобы при этом не развалить дерево и сохранить его сортированность, поступают следующим образом. Для удаляемой вершины ищется ближайшая к ней слева вершина. Для этого нужно сначала перейти от C к ее левому сыну, а затем спускаться направо, пока не попадем в вершину, не имеющую правого сына. В данном примере это вершина D. Далее следует поменять местами удаляемую вершину C и ее левого соседа D (это можно сделать либо путем манипуляций указателями, либо просто обменяв записи таблицы, связанные с вершинами). На новом месте вершина C имеет не более одного сына (ибо правого сына она не имеет), а потому может быть удалена, как в случае а или б. Легко видеть, что сортированность дерева не будет нарушена после этих операций.
Удаление вершин, как и их добавление, может нарушить сбалансированность дерева и в худшем случае привести к его вырожденности.
АВЛ-деревья
Можно ли при работе с бинарными деревьями поиска гарантировать оценку T(n) = O(log(n)) для поиска и вставки не только в среднем, но и в худшем случае? Ответ положительный. Однако для этого следует выбрать подходящий класс деревьев. Для произвольных бинарных деревьев операция вставки выполняется просто и быстро, но поиск может быть долгим в случае вырождения. ИС-деревья гарантируют быстрый поиск, но много времени уходит на поддержание баланса при вставке и удалении. Желательно найти какой-то «средний» тип деревьев, чтобы они были не намного хуже, чем идеально сбалансированные, но вставка выполнялась значительно быстрее.
Было предложено несколько подобных типов деревьев. Среди них АВЛ-деревья [1, 5], 2-3-деревья [3, 5], красно-черные деревья [4]. Мы рассмотрим только АВЛ-деревья, которые были названы в честь предложивших их советских математиков Г.М.Адельсона-Вельского и Е.М.Ландиса и которые до настоящего времени остаются одним из лучших средств решения задачи поиска со вставкой.
АВЛ-деревом[3] называется такое бинарное дерево поиска, для каждой вершины которого высота ее левого и правого поддеревьев отличаются не более, чем на единицу.
Легко видеть, что всякое ИС-дерево поиска является АВЛ-деревом. Обратное, вообще говоря, неверно.
На рис. 4.3 показаны примеры самых худших (т.е. наиболее разбалансированных, «перекошенных») АВЛ-деревьев для различных значений высоты. Как видно из рисунка, даже в худшем случае АВЛ-деревья далеки от вырожденности. Это становится все более заметно при увеличении высоты. Можно доказать, что высота АВЛ-дерева превышает высоту ИС-дерева с тем же количеством вершин не более, чем на 45 %. Таким образом, логарифмическая зависимость высоты от числа вершин сохраняется даже в худшем случае.
Таким образом, качество АВЛ-деревьев вполне приемлемо для быстрого поиска. Покажем, что поддержание сбалансированности при вставке новой вершины для этого типа деревьев требует лишь нескольких операций с указателями.
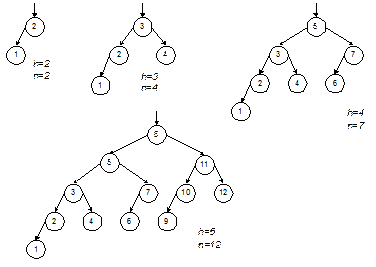
Рис. 4.3. Наихудшие АВЛ-деревья разной высоты
Прежде всего, надо выяснить, каким образом вообще обнаруживается нарушение сбалансированности при вставке. Наиболее удобное решение – хранить в каждой вершине АВЛ-дерева дополнительное поле bal (баланс), которое может принимать одно из трех значений:
t^.bal = –1, если левое поддерево вершины t выше, чем правое;
t^.bal = 0, если оба поддерева одинаковы по высоте;
t^.bal = +1, если правое поддерево t выше, чем левое.
При выполнении вставки сначала происходит рекурсивный спуск по дереву, затем новая вершина добавляется как лист (и для нее, естественно, устанавливается начальное значение bal = 0), а затем, в процессе возврата вверх, для всех вершин соответствующей ветви дерева выполняется корректировка значений поля bal, если вставка новой вершины вызвала увеличение высоты левого или правого поддерева.
Пусть при возврате вверх после вставки выяснилось, что для некоторой вершины C баланс нарушен: левое поддерево C теперь оказалось на 2 единицы выше, чем правое (случай перекоса вправо рассматривается аналогично). При этом для вершин, лежащих ниже C, баланс остается в пределах нормы (от –1 до +1). В этой ситуации возможны два существенно разных случая, проиллюстрированных на рис. 4.4.
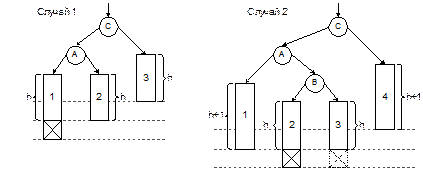
Рис. 4.4. Нарушение баланса при вставке в АВЛ-дерево
Буквой A обозначен левый сын вершины C. Высота поддерева A могла увеличиться либо при вставке в левое поддерево A (случай 1), либо при вставке в правое поддерево (случай 2). Прямоугольники 1, 2, 3, 4 обозначают поддеревья произвольной сложности, а перечеркнутый квадрат – добавленную вершину. Во втором случае показаны два возможных положения добавленной вершины, одно из них – пунктиром. Можно доказать, что в случае 1 высоты поддеревьев 1, 2 и 3 равны одной и той же величине h, а в случае 2 высоты поддеревьев 1 и 4 на единицу больше, чем 2 и 3.
Для восстановления баланса изображенные части дерева должны быть переставлены так, как показано на рис. 4.5.
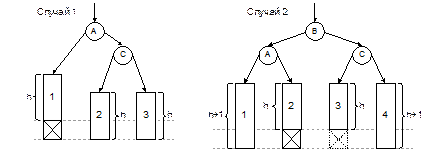
Рис. 4.5. Восстановление баланса АВЛ-дерева
Такие преобразования АВЛ-дерева принято называть его поворотами.
Прежде всего заметим, что повороты не нарушают упорядоченность дерева поиска (например, в случае 1 и до поворота, и после него ключи в различных частях дерева упорядочены следующим образом: 1 £ A £ 2 £ C £ 3). При этом восстанавливается баланс вершин дерева.
Преобразования поворота выполняются с помощью нескольких присваиваний значений указателей. Ниже приведен в качестве примера фрагмент программы, выполняющий поворот для случая 1.
var
t: Tree; {Корень поворачиваемой части дерева}
p: Tree; {Рабочая переменная}
...
p := t^.left; {p -> A}
t^.left := p^.right; {C -> 2}
p^.right := t; {A -> C}
t^.bal := 0; {Оба поддерева C стали одной высоты}
t := p; {A – новый корень повернутой части}
t^.bal := 0; {Оба поддерева A тоже одной высоты}
...
Из сравнения рис. 4.4 и 4.5 можно заметить, что высота рассматриваемой части дерева не увеличивается после вставки и последующего поворота. Это значит, что баланс вышележащих вершин дерева не изменяется и эти вершины не потребуют дополнительных поворотов.
Дата добавления: 2016-03-27; просмотров: 1460;
