Страничные деревья поиска

Использование бинарных деревьев поиска – удачный выбор для решения задачи поиска со вставкой, но только при условии, что все дерево может быть размещено в оперативной памяти компьютера. Однако это не всегда возможно, даже в условиях постоянно возрастающих объемов памяти современных компьютеров. Важный класс задач поиска связан с запросами к базам данных, которые хранятся на периферийных устройствах памяти (дисках и т.п.). При этом, как и в задачах внешней сортировки, рассмотренных в подразд. 3.7, высокая эффективность работы может быть достигнута применением таких алгоритмов и структур данных, которые минимизируют количество обращений к внешней памяти.

С этой точки зрения бинарные деревья представляются малопригодными. Действительно, если не принять специальных мер, то вершины дерева могут оказаться произвольным образом разбросанными по блокам (секторам) устройства, при этом почти каждый переход от вершины-отца к ее левому или правому сыну потребует выполнения операции чтения блока с устройства.

Целесообразно ввести в рассмотрение такие структуры данных (и связанные с ними алгоритмы), которые принимают во внимание блочную структуру хранения данных на устройстве. Действительно, поскольку за одно обращение к диску обязательно читается или записывается сразу блок данных, то алгоритмы поиска должны выполнить максимум полезной работы с этим блоком, прежде чем потребуется перейти к другому блоку. Такие алгоритмы легче конструировать, если физическому понятию «блок» поставить в соответствие некоторую единую структуру данных. Назовем такую структуру страницей.

Ясно, что страница должна содержать намного больше данных, чем вершина бинарного дерева. Типичный размер блока (512 байт для большинства компьютеров) позволяет разместить на одной странице данные, соответствующие нескольким десяткам ключей и указателей. Один из наиболее логичных способов перехода от бинарного дерева к набору страниц показан на рис. 4.6.

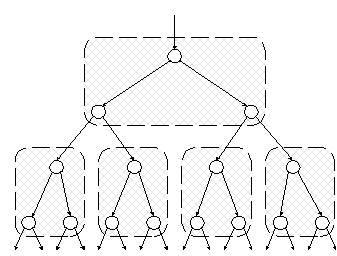
Рис. 4.6. Разбиение бинарного дерева на страницы

Изображенный на рисунке фрагмент сбалансированного бинарного дерева разбит на страницы, которые, ради простоты примера, содержат по три вершины. Разумеется, на практике страница содержит значительно больше данных. Рисунок иллюстрирует две важные особенности разбиения. Во-первых, все страницы представляют собой одинаковые структуры данных. Во-вторых, алгоритм поиска выполняет как можно больше работы на одной странице, прежде чем перейти к другой странице. В данном маленьком примере это выражается в том, что на каждой странице выполняется не одно, а два сравнения ключей.

Теперь посмотрим, что же получилось. Результат разбиения бинарного дерева на страницы схематически показан на рис. 4.7.

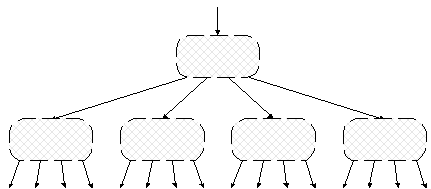
Рис. 4.7. Страничное дерево

Безусловно, это дерево. Но теперь уже не бинарное. Каждая вершина дерева представляет собой страницу, т.е. блок данных на диске, и содержит не два, а большее число указателей на нижележащие вершины-страницы (в данном примере – четыре указателя).

В действительности, страничные деревья далеко не всегда удается так хорошо сбалансировать, как на рисунке. Приходится до определенных пределов мириться и с неполными страницами, и с разной длиной ветвей в дереве страниц.

Рассмотрим подробнее, из чего состоит страница.

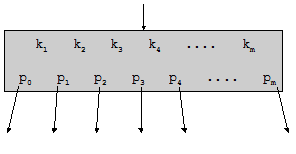
Рис. 4.8. Структура страницы

Как показано на рис. 4.8, страница содержит некоторое количество m ключей k₁, k₂, …, k_m и m+1 указателей на нижележащие страницы p₀, p₁, p₂, …, p_m. Максимальное значение m называется порядком страничного дерева; порядок дерева зависит от размеров страницы, ключа и указателя.

Каждый из p_i указывает на поддерево, содержащее ключи x из определенного диапазона, а именно:

p₀ x £ k₁ ;

p₁ k₁ £ x £ k₂ ;

…

p_i k_i £ x £ k_i+1 ;

…

p_m k_m £ x .

По аналогии с бинарным деревом поиска, описанным в подразд. 4.2, дерево страниц, удовлетворяющее приведенным выше неравенствам, будем называть страничным деревом поиска.

Заметим кстати, что бинарное дерево поиска можно считать частным случаем страничного при m = 1.

Поиск по страничному дереву выполняется следующим образом. Сначала искомый ключ x сравнивается с ключами корневой страницы дерева. При этом либо на странице будет найден ключ k_i = x, либо будет определен интервал (k_i, k_i+1), в который попадает значение x. В этом случае происходит переход по указателю p_i (т.е. фактически с устройства читается другая страница), после чего поиск продолжается. Если дерево не содержит искомого значения x, то на некотором шаге будет получен пустой указатель p_i.

Следует заметить, что слово «указатель» в данном случае не обязательно означает адрес оперативной памяти. Если страничное дерево хранится в файле, то «указатель» будет скорее всего представлять собой смещение указываемой страницы от начала файла (в байтах или в секторах).

Может возникнуть вопрос, как на самом деле расположены ключи и указатели внутри страницы. Судя по рис. 4.6, они образуют бинарное дерево, но на рис. 4.8 размещение больше похоже на два массива. На самом деле, этот вопрос несуществен. Как уже говорилось в подразд. 3.7, операции обмена данными с устройствами выполняются настолько медленнее, чем любые операции в оперативной памяти, что способ организации поиска внутри страницы не оказывает большого влияния на общую скорость поиска. Внутри страницы можно использовать сортированный массив, бинарное дерево или любую другую удобную структуру. Желательно лишь, чтобы эта структура была как можно более компактной, поскольку это позволит увеличить m – число ключей на странице.

Скорость поиска по страничному дереву определяется главным образом числом операций чтения страницы. Поскольку при поиске выполняется спуск от страницы-корня к одной из страниц-листьев, максимальное время поиска определяется высотой дерева. Нетрудно оценить зависимость высоты страничного дерева от общего числа ключей n и порядка дерева m. Введем сначала понятие сбалансированного страничного дерева. Это дерево, все ветви которого по длине различаются не более, чем на 1, и все страницы, кроме, быть может, одной страницы на каждом уровне, содержат ровно m ключей. Можно показать, что высота сбалансированного страничного дерева не превышает log_m(n) + 1. Отсюда понятно, что увеличение порядка дерева приводит к уменьшению высоты дерева, т.е. к ускорению поиска.

Как и в случае бинарных деревьев поиска, многократные операции вставки и удаления ключей в страничное дерево могут, если не принять специальных мер, привести к вырождению дерева. Вырождение заключается в том, что число ключей на страницах становится значительно меньше m, при этом ветви дерева могут сильно различаться по длине. Следствием вырождения будет не только увеличение времени поиска, как в бинарном случае, но и излишний расход дисковой памяти на хранение неполных страниц.

Здесь пора вспомнить, что, помимо ключа, каждая запись таблицы может еще содержать поле данных. На рис. 4.8 поля данных не показаны. Хранение данных внутри страниц дерева может привести к значительному уменьшению значения m (поскольку в одном секторе диска будет помещаться меньше записей). На практике, чтобы не хранить в страничном дереве объемные данные, вместо этого на странице размещают указатель на эти данные, которые хранятся где-нибудь в другом месте (например, в отдельном файле).

B-деревья

Подобно тому, как из множества бинарных деревьев поиска оказалось полезным выделить подкласс АВЛ-деревьев, так и из множества страничных деревьев поиска выделяют подкласс B-деревьев, которые позволяют сочетать достаточно хорошую сбалансированность с возможностью эффективно выполнять операции добавления и удаления ключей.

B-деревом[4] порядка m называется страничное дерево поиска, удовлетворяющее следующим условиям.

1. Каждая страница дерева содержит не более m ключей, причем m – четное число.

2. Каждая страница, кроме, быть может, корневой страницы дерева, содержит не менее m/2 ключей.

3. Все страницы-листья находятся на одинаковом расстоянии от корня.

Условие 1 означает всего лишь, что максимальное число ключей, которые можно разместить на странице, является четным. Условие 2 более существенно: оно означает, что каждая страница дерева (за исключением, может быть, корневой) заполнена по крайней мере наполовину. Условие 3 гарантирует невырожденность дерева.

Условия 1 и 2 кажутся на первый взгляд довольно мягкими. Видно, что они допускают двойной перерасход дисковой памяти по сравнению со случаем дерева, все страницы которого максимально заполнены. Высота B-дерева при этом также не будет минимально возможной. Но это неизбежная плата за компромисс. Как и бинарные АВЛ-деревья, страничные B-деревья не являются оптимальными, но они совмещают достаточно приличную сбалансированность с возможностью быстрой вставки и удаления ключей.

Насколько высота B-дерева (т.е. время поиска ключа) может превышать минимально возможную высоту страничного дерева? Ясно, что высота будет тем больше, чем меньше ключей на каждой странице. Однако можно показать, что при достаточно большом порядке страницы высота наихудшего B-дерева (с одним ключом на корневой странице и m/2 ключами на каждой из остальных страниц) будет лишь на 1-2 уровня превышать высоту наилучшего дерева (с m ключами на каждой странице).

Рассмотрим теперь, как выполняется добавление новых ключей в B-дерево и каким образом при этом достигается соблюдение условий 1 – 3.

При поиске ключа в B-дереве происходит спуск от корня до страницы, содержащей искомый ключ. Если ключ не найден, то поиск завершается на той странице-листе, куда следует вставить этот ключ.

На рис. 4.9 показано небольшое B-дерево порядка 4, в которое последовательно вставляются три ключа.

Рис. 4.9. Добавление ключей в B-дерево

На верхнем рисунке – исходное B-дерево. При вставке на шаге 1 ключа 4 поиск приведет на крайнюю левую страницу-лист и, поскольку на странице есть свободное место, ключ добавляется без проблем.

На шаге 2 ключ 6 должен быть вставлен на ту же страницу, но места там уже нет. В этом случае должна быть выполнена операция расщепления страницы. Она заключается в следуюшем. Создается новая страница дерева. Те m ключей, которые были на заполненной странице (2, 4, 5 и 7), плюс вставляемый ключ 6, распределяются так: меньшие m/2 ключей (2 и 4) остаются не прежней странице, большие m/2 (6 и 7) переносятся на новую. Средний по значению ключ 5 переносится на страницу уровнем выше и используется как разделитель двух нижних страниц.

Из приведенного описания становится понятно, откуда взялось число m/2 в определении B-дерева.

На шаге 3 ключ 18 также должен быть вставлен в заполненную страницу с ключами 11, 12, 16 и 19. При расщеплении на старой странице остаются ключи 11 и 12, на новую переносятся 18 и 19, а ключ 16 переносится на уровень вверх, на корневую страницу, где для него опять нету места. Создаются еще две новые страницы, одна из которых становится новым корнем B-дерева, содержащим всего один ключ. Высота дерева в этом случае увеличивается на 1.

В худшем случае при добавлении одного ключа переполнение страниц может приключиться на каждом уровне дерева, что приведет к созданию h+1 новой страницы. Но после этого на всех затронутых расщеплением страницах будет полно свободного места, так что следующее переполнение вряд ли случится скоро. Так или иначе, время вставки пропорционально высоте дерева, т.е. логарифму от числа вершин.

Заметим, что на шаге 3 можно было бы избежать расщепления страниц, воспользовавшись операцией переливания ключей на соседнюю неполную страницу. Рядом со страницей, содержащей ключи (11, 12, 16, 19), имелась страница с ключами (25, 26). При добавлении ключа 18 на старой странице можно было бы оставить ключи (11, 12, 16, 18), ключ 19 перешел бы вверх на место ключа 20, который сдвинулся бы вниз: (20, 25, 26). Если использовать переливание, то расщепление страницы будет необходимым только тогда, когда ни слева, ни справа от переполняющейся страницы нет страницы со свободным местом.

Удаление ключа из B-дерева можно рассматривать как обратную операцию по отношению к вставке, однако здесь имеются некоторые дополнительные сложности. При удалении ключа надо обязательно сделать попытку переливания с одной из соседних страниц и только в случае невозможности следует объединять две страницы в одну, перенося вниз разделяющий их ключ со страницы верхнего уровня. Переливание выполняется не только для страниц-листьев, но и для внутренних страниц, если число ключей стало меньше m/2.

Описанная выше модель B-деревьев допускает многочисленные варианты и улучшения. Вероятно, самое главное уточнение заключается в следующем. Обратим внимание, что структура страниц-листьев отличается от остальных страниц дерева. Из листьев не выходят указатели на нижележащие страницы, значит для указателей не нужно отводить место на странице. Сэкономленная память может быть использована для хранения большего количества ключей и данных на каждой странице-листе. Это приведет к уменьшению общего числа страниц, и как следствие, – к уменьшению высоты дерева.

Можно также повысить порядок внутренних страниц B-дерева, если отказаться от хранения данных на всех страницах, кроме листьев. Тогда внутренние страницы будут содержать только ключи и указатели на нижележащие страницы, а листья – ключи и связанные с ними данные. При этом, очевидно, листья будут содержать все записи таблицы, т.е. все ключи и их данные, а внутренние листья тогда должны содержать дубликаты некоторых ключей, позволяющие спуститься к нужному листу. Такая структура данных называется B+-деревом. Пример B+-дерева показан на рис. 4.10.

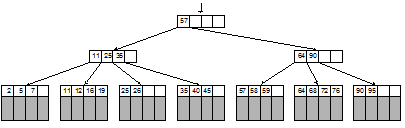
Рис. 4.10. Структура B⁺-дерева

На рисунке серым заштрихованы области памяти, отведенные для хранения данных, связанных с ключами. Можно отметить, что каждый ключ, расположенный во внутреннем узле дерева, является дубликатом ключа ближайшей к нему справа записи, расположенной в листе дерева[5].

В тех случаях, когда объем внешней памяти ограничен и потому нежелателен двойной перерасход памяти, допускаемый моделью B-деревьев, можно использовать такую модификацию, как B*-деревья. Они отличаются иным алгоритмом вставки (и удаления) ключей. В этом алгоритме при переполнении страницы обязательно используется переливание на одну из соседних страниц. Когда соседние страницы заполнены, выполняется расщепление не одной страницы, а двух соседних страниц. На новую страницу переносится треть ключей с каждой из двух заполненных страниц, так что каждая страница B*-дерева будет заполнена по крайней мере на 2/3, а не на 1/2, как для обычного B-дерева. Корневая страница B*-дерева должна при этом быть большего размера, чем остальные, и она может быть заполнена не более чем на 4/3 от объема обычной страницы. При расщеплении корня он дает две обычные страницы, заполненные на 2/3, а новый корень, как и для B-деревьев, содержит только один ключ.

Модель B*-деревьев позволяет сократить расход внешней памяти примерно на 25 %, но при этом добавление и удаление ключей выполняется заметно сложнее, чем для B-деревьев.